| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 10990 | cheat sheet |
|
| 12711 | Parentheses Tree |
|
| 12725 | Minimum Spinning Tree |
|
Description
Linked list
typedef struct _Node {
int data;
struct _Node *next;
} Node;
/* print the content of the linked list.*/
void printList(Node *head)
{
Node *temp;
for(temp=head; temp!=NULL; temp=temp->next) {
printf("%d ", temp->data);
}
}
/*Insert a node after the node pointed by nd.
Return 1 if insertion succeeds.
Otherwise, return 0.*/
int insertNode(Node* nd, int data)
{
if (nd != NULL) {
Node* temp = (Node*)malloc(sizeof(Node));
temp->data = data;
temp->next = nd->next;
nd->next = temp;
return 1;
}
return 0;
}
/*Delete a node after the node pointed by nd.
Return 1 if insertion succeeds.
Otherwise, return 0.*/
int deleteNode(Node* nd)
{
if (nd != NULL) {
Node* temp = nd->next;
if (temp != NULL) {
nd -> next = temp->next;
free(temp);
return 1;
}
}
return 0;
}
Binary tree
typedef struct _node {
int data;
struct _node *left, *right;
} BTNode;
Tree traversal
- Pre-order: visit root, left subtree, and right subtree
- In-order: visit left subtree, root, and right subtree
- Post-order: visit left subtree, right subtree, and root
Expression order
- Prefix: operator, left operand,and right operand
- Infix: left operand, operator, and right operand
- Postfix: left operand, right operand, and operator
Syntax tree
The internal nodes are operators, and the leaves are operands.
Recursive evaluation of prefix expression
/*It is a pseudo code */
int evalBoolExpr(){
char c = getchar();
If c is an operator
op1 = evalBoolExpr();
op2 = evalBoolExpr();
return op1 c op2;
Else if c is a variable
return the value of c;
}
Grammar of infix expression with parenthesis
- EXPR = FACTOR| EXPR OP FACTOR
- FACTROR = ID | (EXPR)
/*Suppose expr[] is an array of expression and pos is the current position, which initially is strlen(expr)-1. */
/*-------------------------------------*/
BTNode* makeNode(char c)
{
int i;
BTNode *node = (BTNode*)malloc(sizeof(BTNode));
set node->data
node->left = NULL;
node->right = NULL;
return node;
}
/*-------------------------------------*/
BTNode* FACTOR()
{
char c;
BTNode *node = NULL;
if (pos>=0) {
c = expr[pos--];
if (c is an ID) {
node = makeNode(c);
} else if (c==‘)’) {
node = EXPR();
if(expr[pos--]!= '(') {
printf("Error!\n");
freeTree(node);
}
}
}
return node;
}
/*-------------------------------------*/
BTNode* EXPR()
{
char c;
BTNode *node = NULL, *right=NULL;
if (pos>=0) {
node = right = FACTOR();
if (pos>0) {
c = expr[pos];
if (c is an operator) {
node = makeNode(c);
node->right = right;
pos--;
node->left = EXPR();
}
}
}
return node;
}
Input
Output
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Parentheses are at the heart of programming.
Understand parentheses and you can rule the earth.
by Mike James
To construct a unique binary search tree, the in-order and pre/post-order traversal sequences are both required.
However, it takes too much memory in some applications.
Mike came up with a genius solution: use parentheses to represents a unique binary tree.
A tree can be represented like: Tree = ( data LeftSubTree RightSubTree ) if the data exisit. Otherwise, Tree = () which means the tree contains nothing.
For example:
- () = NULL
- (3()())


- (2(1()())(3()())):


- (1()(2()(3()()))):


Given a valid parentheses tree expression.
Your task is to bulid the tree from it, and output the inorder and postorder traversal sequences. Then you can rule the earth.
Input
The first line contains N, denoting the length of parentheses expression.
The second line contains the parentheses representation for a unique tree.
It is guaranteed that:
- 2 ≤ N ≤ 106
- The number of each Node is in the range of
int.
Output
Output the in-order and post-order traversal sequence for the tree on the first and second line.
Every number is followed by one space.
Remember '\n' on the end of each line.
Tree of Sample IO


Sample Input Download
Sample Output Download
Tags
Discuss
Description
Disclaimer : This problem has nothing to do with MST(Minimum Spanning Tree). You don't need solid algorithm basic to solve this problem.
After doing a bunch of dull tree problems, you become dizzy and the trees look like they are spinning in your view.

You see an expression tree. The tree in your view can spin in two directions:
-
Left Spin: For a tree rooted at node P, of which right child is node Q and the left child of Q is B, after a left spin, the new root becomes Q, the left child of Q becomes P, and the right child of P becomes B. If P doesn't have a right child (i.e. Q is null), left spin cannot be performed. -
Right Spin: For a tree rooted at node Q, of which left child is node P and the right child of P is B, after a right spin, the new root becomes P, the right child of P becomes Q, the left child of Q becomes B. If Q doesn't have a left child (i.e. P null), right spin cannot be performed.
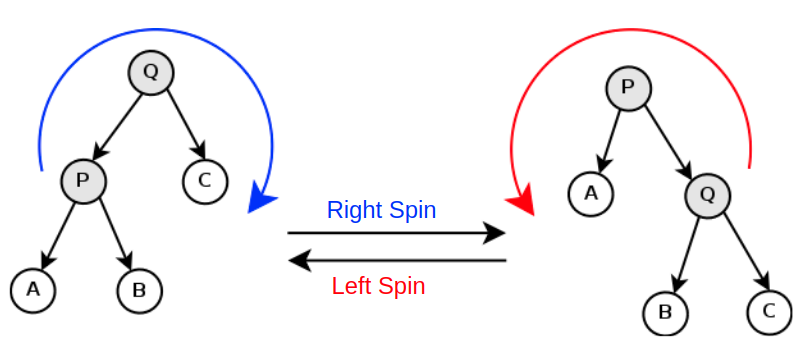
After several (or zero) times of spinning, if the expression tree can still denote a valid expression, we say that the tree is a good spinning tree; otherwise we say that the tree is a bad spinning tree.
The evaluation of the tree changes after the tree spins. Given an evaluation tree, you want to know that what is the minimum evaluation among all good spinning trees.
Explanation of Sample IO
For the given expression tree, it has four good spinning trees which are shown in the below figure. Initially its evaluation is -8. After one left spin, its evaluation becomes 0. After two left spins, its evaluation becomes -6. After one right spin, its evaluation becomes 0. It is obvious that after three left spins or two right spins, the tree cannot donate a valid expression. Therefore the minimum spinning tree is the inital tree and therefore output -8.
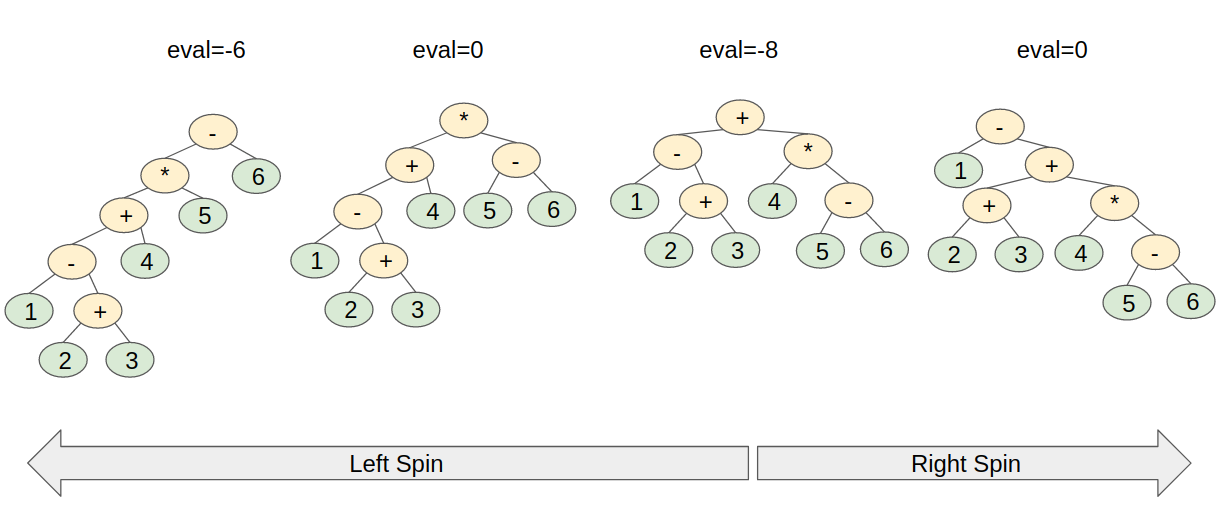
Input
The first line of the input is an integer N(3 <= N <= 3x105), being the length of the prefix expression of the expression tree.
The next line is the expression tree (in prefix expression). The expression contains only +, -, * and digits. All the numbers in the expression are integers between 1 and 9.
Test Cases
-
For all test cases, it is guaranteed values during calculation is between [-109, 109], meaning that using 32-bit integer will not overflow (if your code does not have bugs).
-
1-st test case : same as sample IO
-
2-nd test case : N <= 50. It is guaranteed that there are only three good spinning trees : the giving tree, the tree that left spins once, and the tree that right spin once. (i.e. evaluate the three good spinning trees and output the minimum value, and then you get AC in this test case)
-
3-rd, 4-th test case : You can get AC using an O(N2) solution.
-
5-th test case : You need to come up with an O(N) solution to get an AC.
Output
Output the minimum evaluation among all good spinning trees.
Note that you should have a '\n' in the end.