| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11443 | 3DShape |
|
| 12765 | Big Pascal Triangle |
|
Description
Warning: You are not allowed to use malloc and free
Giving a bass-class Shape3D and 4 derived class : Sphere (球體), Cone (圓錐), Cuboid (長方體), Cube (立方體)
You need to calculate the volume of each shape.
PS:
V of Sphere: V = 4/3 π r3
V of Cone: V = 1/3 π r2 h

note : Remember to do some basic check, if the input is illegal (e.g. length < 0, pi < 0 .....) then the volume should be 0.
You don't need to consider the scenario like Cuboid -1 -2 3, volume would be 0 instead of 6.
Hint1: Be careful the type of volume is double. 4/3=1 (int), so it should be 4.0/3.0
Hint2: You only need to implement the constructors.
Hint3: Note that Cube inherited Cuboid not Shape3D.
Input
There are only 4 shapes in this problem :
- Sphere, following by its radius and pi. (e.g. Sphere 30 3.14)
- Cone, following by its radius of bottom plane, height and pi. (e.g. Cone 3 100 3.14)
- Cuboid, following by its length, width and height. (e.g. Cuboid 2 3 7)
- Cube, following by its length. (e.g. Cube 2)
Output
Ouput the total volume of all the shapes.
Sample Input Download
Sample Output Download
Partial Judge Code
11443.cppPartial Judge Header
11443.hTags
Discuss
Description
A pascal triangle is a triangle full of numbers in the following rule:
-
The left most number and right most number of each row is 1
-
For the rest of the numbers, they are the sum of the two numbers directly above it
The following is a picture of a pascal triangle with height = 5.
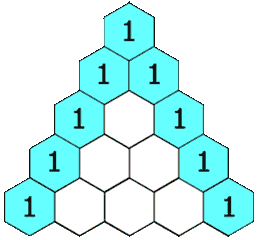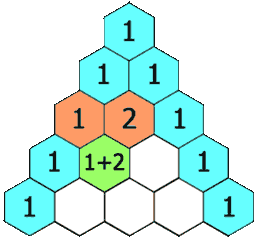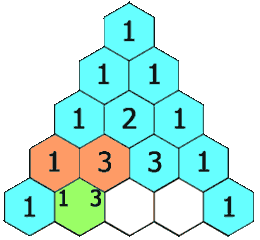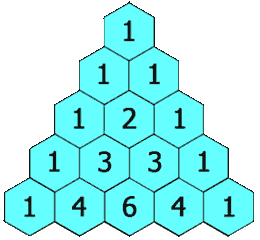
Given a pascal triangle with height h, please calculate the sum of all numbers in the pascal triangle.
Since the sum is very large, it is suggested to implement a Big Integer class to calculate the answer. For sample code of Big Integer class, please refer to hw4.
Hints and Reminders
-
Try to observe the sum of each row in the pascal triangle
-
Be careful of overflow while implementing big integer
-

Input
The first line contains a single integer T, meaning that there are T test case in one input.
Then there are T lines, each lines contains a single integer h, begin the height of pascal triangle.
-
1 <= T <= 100
-
1 <= h <= 100000
Output
For each test case, output sum of all numbers in the pascal triangle in a line.