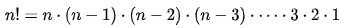| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12396 | Walking Up Stairs |
|
| 12908 | Number of factorial’s factors |
|
| 12909 | Big number subtraction |
|
Description
Your friend likes walking up stairs.
He likes walking up stairs so much that everytime, he attempts to walk up stairs in a way he never did before.
When walking up stairs, he either takes one step up or three steps up at once.
Specifically, given a staircase with N levels, he would decide a sequence of steps (composed of 1s and 3s) to take, such that the sum of the sequence is N.
Two ways of walking up stairs are different if and only if the sequence of steps differ.
For example, given a stairs with 5 floors, he has 4 unique ways of walking up the stairs:
a. [1, 1, 3]
b. [1, 3, 1]
c. [3, 1, 1]
d. [1, 1, 1, 1, 1]
Given N, find out how many times your friend may enjoy walking the stairs up in a unique way.
Smart as your friend is, figured out that f(n), the number of ways to walk up n levels, may be described as the following:
f(n) = f(n - 1) + f(n - 3), if n > 2
f(n) = 1, otherwise
Input
N
(N is a positive integer in between 1 and 116)
Output
A positive integer indicating the number of unique ways to walk up the stairs, with a trailing newline character.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In mathematics, the factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n:
For this question, you are asked to compute the number of the given factorial's factors.
For example:
4! = 4 × 3 × 2 × 1 = 24
factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Therefore, you should output 8 as the answer.
[HINT]
You should not directly calculate the answer of n!, or even unsigned long long cannot store your answer.
The best way to solve this question is to use the prime number ≤ N to do prime factorization and then use the result of it to get the final answer.
For example:
4! = 23 × 3, so the number of 4! 's factors = (3+1) × (1+1) = 8
Input
One interger N which denotes the given factorial of N.
(Note that 2 ≤ N ≤ 100)
Output
One integer which denotes the number of the given factorial's factors.
Note that you don't need to print '\n' at the end of the output
(We guarantee that the answers can be stored into unsigned long long)
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In the most of arithmetic subtraction case, we can simply use int or long long to store the two integers and compute the answer by the operater ' - ' in C. If we have two big integers that can not be stored into the varibles mentioned below, we should make use of arrays to complete the subtraction task.
Given two big number A, B, please compute A - B.
[Hint]
To solve this problem, we can imitate the straight addition we have learned in elementary school. Here are some tips:
1. Use arrays to store the two big numbers, and then subtract them one by one from low digit to high digit.
2. If A > B, you can directly switch them and add ' - ' in the final answer to make the calculation easy.
(This problem is a little bit hard. If you have no idea, you can google "Big number subtraction" to learn the implementation detail.)
Input
First line contains an integer which denotes the length of A. The following one line contains the big integer A.
Third line contains an integer which denotes the length of B. The following one line contains the big integer B.
(1 ≤ number of digits of A, B ≤ 100, both A and B are positive integers)
Output
An integer which denotes the answer of A -B. (Answer can be negative)
Note that you don't need to print '\n' at the end of the output