| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12443 | Permutations |
|
| 12486 | Tower of Hanoi |
|
| 12964 | Sierpiński carpet |
|
| 12965 | Combinations |
|
Description
A permutation, also called an “arrangement number” or “order,” is a rearrangement of the elements of an ordered list into a one-to-one correspondence S_i. A string of length N has N! permutation. You need to show all results.
ORDER is important !! You should display it in lexicographic order.
ex. N=3,
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
Input
N
1<=N<=6
Output
S_i is a sequence each element followed by a space.
S_1
S_2
.
.
.
S_N!
You still need to change line in the last line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
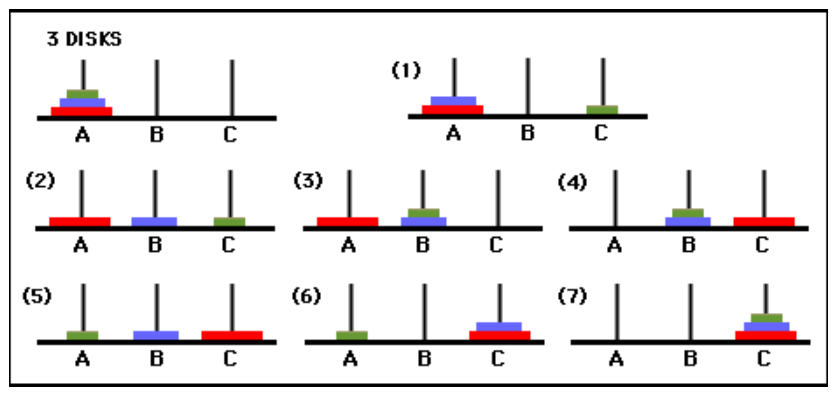
The Tower of Hanoi is a mathematical game puzzle. It consists of three rods, which are A, B and C. The puzzle starts with n disks in ascending order of size on rod A, the smallest at the top.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.
Write a program to simulate the optimal moves of the disks. Print the number of disk which is moved in each step.
For example, if n = 3, the moves of each steps are:
move disk 1 from rod A to rod C
move disk 2 from rod A to rod B
move disk 1 from rod C to rod B
move disk 3 from rod A to rod C
move disk 1 from rod B to rod A
move disk 2 from rod B to rod C
move disk 1 from rod A to rod C
HINT : You can modify this sample code and implement the function 'hanoi'
#include <stdio.h>
void hanoi(int n, char A, char B, char C);
int main(){
int n;
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
Input
An integer n (0<n<20), which means the number of disk.
Output
Print out the information of each step, and there is a '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Sierpiński carpet is a pattern that can generate by recursion.
The construction of the Sierpiński carpet begins with a square (its side length is the power of 3 and all the grids are coloerd white). The square is cut into 9 congruent subsquares in a 3-by-3 grid, and color the central subsquare by black. The same procedure is then applied recursively to the remaining 8 subsquares. Terminates when it recurse to the 1 by 1 square.
For instance, the following figures are the Sierpiński carpet with side length 3 and 9.


The following fugure is the Sierpiński carpet with side length 27.

Input
Input contains single integer n (1 <= n <= 7).
Output
Please output the Sierpiński carpet of side length 3n and use '.' to represent white, '#' to represent black.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The testcases of this problem have been update at 2020/11/14 18:26. Sorry for the inconvenience.
A combination is a selection of items from a collection, such that the order of selection does not matter (unlike Permutations).
You have to write a program to output all combinations of choosing M items from the given array A whose size is N.
Input
First line contains two integers N, M (1 <= M <= N <= 22).
Second line contains N distinct integers Ai (1 <= Ai <= 100) sorted by ascending order.
Output
Output all the n choose m combinations by lexicographic order.
For each combination, you must print it with ascending order and seperated by a space.
Remember to add a newline character('\n') at the end of every line.