| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11200 | Tower of Hanoi |
|
| 12991 | Toad Jumping |
|
Description
The Tower of Hanoi is a mathematical game puzzle. It consists of three rods, which are A, B and C. The puzzle starts with n disks in ascending order of size on rod A, the smallest at the top.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.
Write a program to simulate the moves of the disks. Print the number of disk which is moved in each step.
For example, if n = 3, the moves of each steps are:
move disk 1 from rod A to rod C
move disk 2 from rod A to rod B
move disk 1 from rod C to rod B
move disk 3 from rod A to rod C
move disk 1 from rod B to rod A
move disk 2 from rod B to rod C
move disk 1 from rod A to rod C
You should print out:
1
2
1
3
1
2
1
HINT : You can modify this sample code and implement the function 'hanoi'
#include <stdio.h>
void hanoi(int n, char A, char B, char C);
int main(){
int n;
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}
Input
An integer n (0<n<20), which means the number of disk.
Output
Print out the number of disk which is moved in each step, and there is a '\n' at the end of each line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
There are N stones on the river. The height of the i-th stone is hi for 1 <= i <= N and is colored with color ci. Toad Epep is on the S-th stone (where the leftmost stone is the 1-st stone) and he wants to go the the T-th stone with several jumps.
For each jump from the i-th stone, Epep can jump to the (i-1)-th stone (if it exists), the (i+1)-th stone (if it exists), or any stone colored with the same color ci (if it exists).
Epep will only visit each stone at most once. That is, if Epep jumped to the k-th stone at some time, he won't jumped to the k-th stone again.
The energy cost of jump from i-th to j-th stone is |i-j| x |hi - hj|.
Because Epep ate too much insects and wants to do more exercise, can you help Epep to find the way that cost the most energy (if there are several ways with same maximum energy cost, find the way with maximum jumps) ?
Explanation of Sample IO
All possible moves are listed in the following:
-
2 -> 1 -> 4 -> 3 -> 6 -> 5, which costs 100 energy and 5 jumps
-
2 -> 1-> 4 -> 5, which costs 60 energy and 3 jumps
-
2 -> 3-> 4-> 5, which costs 40 energy and 3 jumps
-
2 -> 3 -> 6 -> 5, which costs 40 energy and 3 jumps
-
2 -> 5, which costs 0 energy and 1 jump
Hint:
1. In this problem, you may need to use an array int jumped[N+1] to record whether a stone i has been visited in the currently expanded path.
2. However, you need to manipulate the int jumped[N+1] array properly as follows:
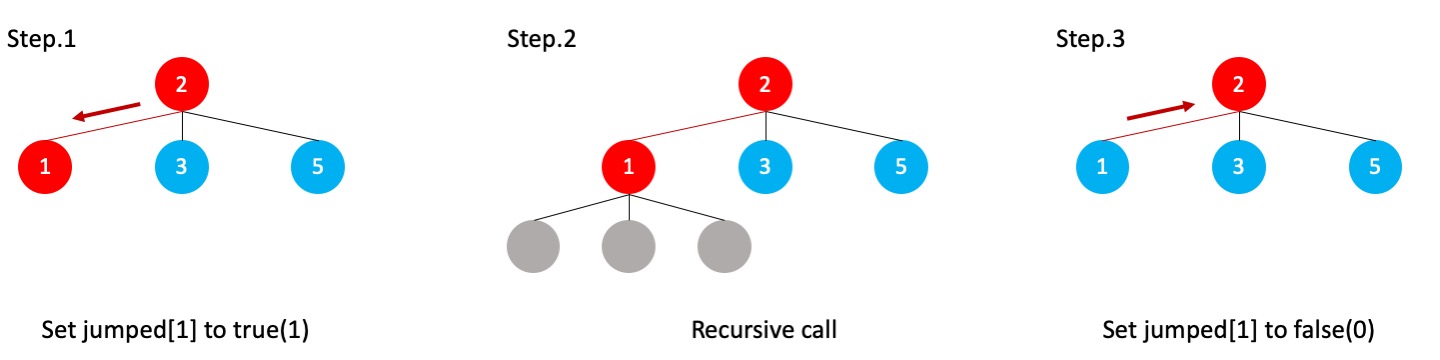
Input
Integers N, S, T are on the first line.
h1, ..., hN are on the second line.
c1, ..., cN are on the third line.
-
1 <= N <= 15
-
1 <= S, T <= N and S != T
-
1 <= hi <= 100000
-
1 <= ci <= 15
Test case description
-
Test case 1: all stones have different colors
-
Test case 2: all stones have the same color
-
The remaining test cases: no additional restrictions
Output
Output two integers E and J, where E is the maximum energy cost and J is the number of jumps in one line. Remember to add \n in the end.