| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 10966 | Infix to syntax tree |
|
| 10968 | Prefix to infix |
|
| 10972 | Remove unnecessary parentheses |
|
| 11339 | linked list-insert, erase and remove |
|
| 11847 | Prefix Boolean expression |
|
| 12183 | Fairy Testing |
|
| 12193 | Binary Search Tree Operation |
|
| 13130 | Kuo Wants Prufer Code |
|
| 13132 | KuoYangてぇてぇ — Birthday Present |
|
Description
Given an infix Boolean expression with parentheses, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. Build a corresponding syntax tree for it.
To parse the infix expression with parentheses, use the grammar below.
EXPR = FACTOR | EXPR OP FACTOR
FACTOR = ID | (EXPR)
EXPR is the expression, ID is one of ‘A’, ‘B’, ’C’, or ‘D’, and OP is one of ‘&’ or ‘|’.
You will be provided with main.c and function.h. main.c contains the implementation of functions printPrefix and freeTree. function.h contains the definition of tree node and variables. You only need to implement the following three functions in function.c.
BTNode* makeNode(char c) // create a node without any child
BTNode* EXPR() // parse an infix expression and generate a syntax tree
BTNode* FACTOR() // use the parse grammar FACTOR = ID | (EXPR) to deal with parentheses
For OJ submission:
Step 1. Submit only your function.c into the submission block.(Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
The input contains N infix expressions, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, two operators ‘&’ and ‘|’, and parentheses. All parentheses are matched.
Output
The output contains N prefix expressions without parentheses, which are preorders of syntax trees.
Sample Input Download
Sample Output Download
Partial Judge Code
10966.cPartial Judge Header
10966.hTags
Discuss
Description
Given an prefix Boolean expression, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. Output its infix presentation with necessary parenthesis.
- Ex: input: ||A&BCD
output: A|(B&C)|D
Hint : About necessary parenthesis, you can observe the syntax tree which has been constructed, then you will find out the rule. For example, the infix expression of |&|AB&CDA with necessary parenthesis is A|B&(C&D)|A, rather than (A|B)&(C&D)|A .
- Syntax tree of |&|AB&CDA
You will be provided with main.c and function.h, and asked to implement function.c.
For OJ submission:
Step 1. Submit only your function.c into the submission block.(Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
The first line will have a number N with the number of test cases, followed by N lines of input, each contain the prefix Boolean expression.
Output
There are N lines infix expression with necessary parenthesis.
Sample Input Download
Sample Output Download
Partial Judge Code
10968.cPartial Judge Header
10968.hTags
Discuss
Description
Given an infix Boolean expression with parentheses, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. Please remove unnecessary parentheses and print the infix expression. Existence of unnecessary parentheses doesn’t affect the result of expression. For example,
(A&B)|(C&D) → A&B|(C&D)
(((A|B))) → A|B
Hint: You can combine two homework. Build a syntax tree and print the infix expression with necessary parentheses.
For OJ submission:
Step 1. Submit your main.c into the submission block.(Please choose C compiler)
Step 2. Check the results and debug your program if necessary.
Input
The input is an infix expression, which has at most 4 variables ‘A’, ’B’, ‘C’, and ‘D’, two operators ‘&’ and ‘|’, and parentheses. The length of the infix expression is less than 256.
Output
The output is an infix expression without unnecessary parentheses.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
This problem will ask you to do some operations on a list. These operations contains insert, erase, print, remove and show. The position of first node is 0.
Input
The input consist of a number of operations. The first line specifies a non-negative integer N that specifies the number of operations. Each operations (I, E, P, R and S) are separated by a newline character (\n).
I stands for “insert”, following by a non-negative integer (insert position) and a non-negative integer (insert value, 0<=insert value<65536). Insert a node at insert position with insert value.
E stands for “erase”, following by a non-negative integer (start position) and a non-negative integer (end position). End position must be greater than or equal to start position. Erase multiple nodes from start position to end position (excluding end position). If start position is equal to end position, do not erase end position.
If any input positions in the two operations above is greater than or equal to the length of the list, treat the input position as the next position of the last position at the list.
For example, input is
I 0 0
I 1 1
S
Output should be
0 1
P stands for “print”, following by a non-negative integer (print position). Print the value of the node at print position.
If print position is greater than or equal to the length of the list, treat the input position as the last position at the list. If the
linked list is empty, do not print anything.
R stands for “remove”, following by a non-negative integer (remove value). Remove the nodes in the list with the value that is equal to remove value.
S stands for “show”. Print the value of all nodes in the list. Separate every prints by a whitespace character. If the list is empty, do not print anything.
For example, input is
5
E 1 1
E 1 2
P 2
R 1
S
Output should be nothing.
Output
Print a space after doing P or S operations (if P or S has printed something).
Sample Input Download
Sample Output Download
Partial Judge Code
11339.cPartial Judge Header
11339.hTags
Discuss
Description
Give a prefix Boolean expression, which only has at most 4 variables ‘A’, ‘B’, ‘C’, and ‘D’, and 2 operators, AND ‘&’ and OR ‘|’, print its truth table.
For example, if input is "|&AC|AB", then result will be
A B C D output
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 1
0 1 0 1 1
0 1 1 0 1
0 1 1 1 1
1 0 0 0 1
1 0 0 1 1
1 0 1 0 1
1 0 1 1 1
1 1 0 0 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
Input
The input contains a sequences of prefix expression. It only has at most 4 variables ‘A’, ‘B’, ‘C’, and ‘D’, and 2 operators, AND ‘&’ and OR ‘|’. The length of prefix expression is shorter than 30.
Output
It has 5 variables 'A', 'B', 'C', 'D', and output, each variable is separated by a space.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In this problem, you are given a prefix Boolean expression, which has at most N=10^5 variables and 2 kinds of operators ‘&’ and ‘|’. Each variable has an ID number. The values of these variables can be either 0 or 1, and are all initialized as 0.
You will be given M ID numbers. For each ID number, you should flip (0 will become 1, 1 will become 0) the value of the corresponding variable and then compute/output the result of the prefix Boolean expression.
Example:
Assume the prefix Boolean expression is &[1][2] and the given ID numbers are “2 1”. First the value of variable 2 will change from 0 to 1. The output of &[1][2] is 0&1=0. Next, the value of variable 1 will change from 0 to 1. The output of &[1][2] is 1&1=1.
Hint: (You can go to the Input/Output description directly, and come back for hints if necessary.)
Hint 1: To solve this problem, you can parse the input and derive the output recursively each time a variable is flipped. Unfortunately, this brute-force approach is not efficient and can lead to TLE, in particular the 3rd and 4th testcases in this problem. We encourage you to use the syntax tree of the prefix Boolean expression for better efficiency.
Hint 2: The key idea behind the syntax-tree approach is to avoid re-evaluation of the whole expression every time a bit is flipped. Some more hints are provided for you as follows:
- [Data structure] Use a tree node pointer array to record the address of each variable (leaf) node of the syntax tree: you can locate each variable to be flipped directly;
- [Data structure] For each tree node i, record the value of its subtree (rooted at node i);
- [Algorithm] Starting from the variable node to be flipped, move upward following the syntax tree and update the node values until the output of the syntax tree (or the Boolean expression) can be determined.
Example:
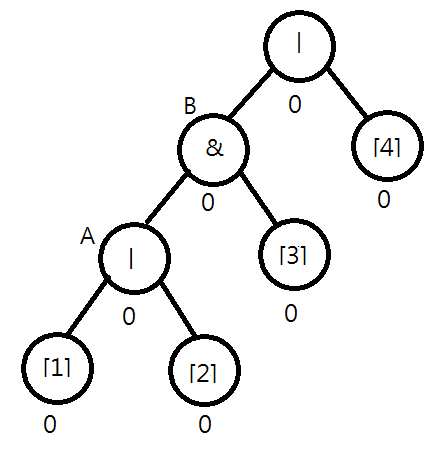
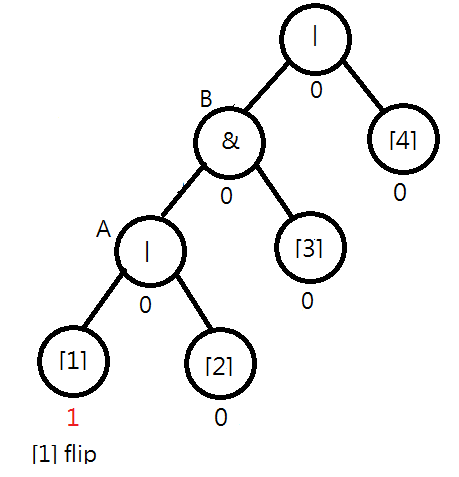
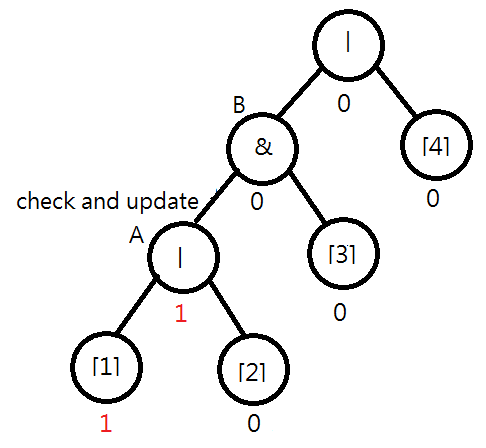
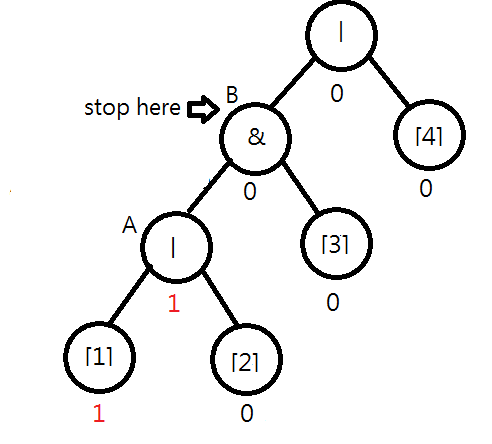
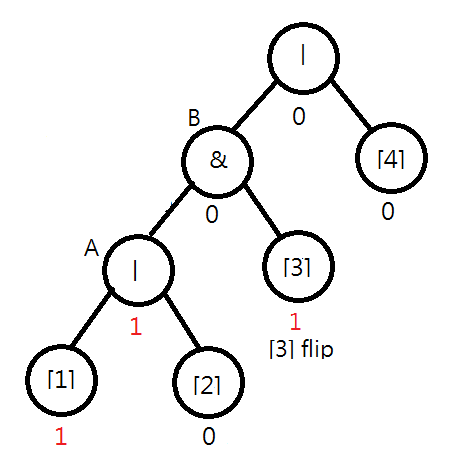
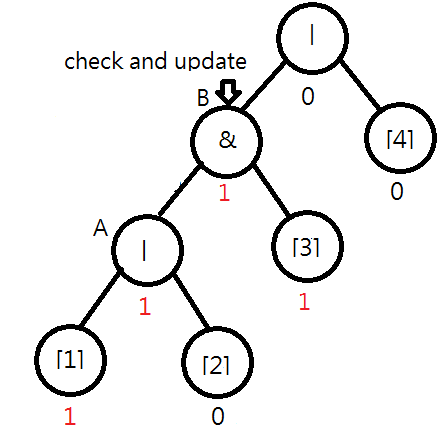
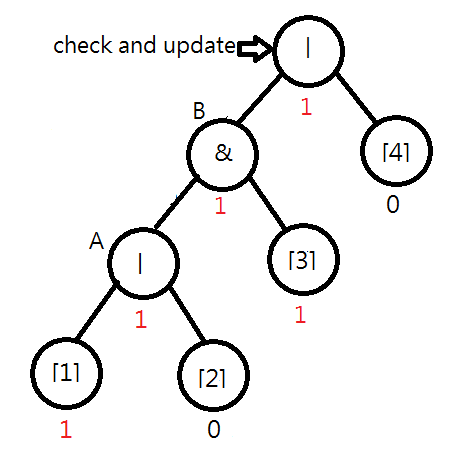
Consider the following syntax tree for "|&|[1][2][3][4]". Assume [1] is flipped. You will find that the value of node A should be changed to 1|0=1. Moreover, you note that the value of B remains unchanged, i.e., 1&0=0, and the checking process can stop.
Later, when [3] is flipped, both the values of node B and the root node should be changed. In this case, the output is also changed.
Sample structure:
typedef struct node{
int value; // This is the value of the subtree, not the ID number
int tokentype;
struct node *leftchild;
struct node *rightchild;
struct node *parent; //pointing to the parent node
}Node;
Node* variable[100001]; // This array stores the pointers pointing to the tree nodes. For example, variable[0] points to the node with ID number 0.
Input
The first line has one number T, 0<T<= 7, indicating the number of testcases.
The following lines are the inputs of the testcases.
Each testcase contains three lines:
1. N, M (0<N<=100000, indicating the number of variables in a given prefix Boolean expression. 0<M<=100000, indicating how many times the values are flipped).
2. A string S, describing the prefix Boolean expression (& means and gate, | means or gate, [i] means a variable ID)
3. M numbers, where each number i means the value of variable i is flipped. The order matters.
Note that all the variables are initially 0.
Each ID number only appears once in the prefix Boolean expression.
The depth of the tree is no more than 30.
Output
For each testcase, you should output M lines, each showing the output of the prefix Boolean expression after a variable is flipped.
0 for false, 1 for true.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The problem will ask you to create a binary search tree, and there will be 4 kinds of commands to complete
1. P : please print out the binary search tree in in-order form in th line ,if the tree is empty, please print "NULL"(There is an whitespace between each number, also after the last number,no space after NULL)
2. GetMax : print out the maximum height of the binary search tree( There need no space after output number)
3. SumLevel (input) : print out the sum value of the nodes at the input level in the line, if the input level is bigger than the maximum height, please print out "0". ( There need no space after output number)
4. AverLevel (input) : print out the average value of the nodes at the input level in the line, please show only 3 digits after decimal point of the average numbers of level, if the input level is bigger than the maximum height, please print out "0". (You can simply use %.3f to display in such way) ( There need no space after output number)
the root level will represent as 1( for SumLevel & AverLevel, if the input level is 0, please print "0")
Input
The first line contains an integer N , which indicates the number of nodes of the binary search tree.
The second line is the data for create binary search tree
The third line contains an integer M , which indicates the number of commands.
Following line will be the input instruction
If there is same input value, please ignore the second one.
Output
There need to print newline in the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Given a tree with n labeled nodes with labels from 1 to n, a Prufer code uniquely idetifies the tree by the following rule.
At step i, remove the leaf (the nodes with deg = 1) with the smallest label and set the i-th element of the Prüfer sequence to be the label of this leaf's neighbor until only two nodes left.
For example, the Prufer code of the tree below is {4, 4, 4, 5}. (the order of the leaf removed is 1, 2, 3, 4)
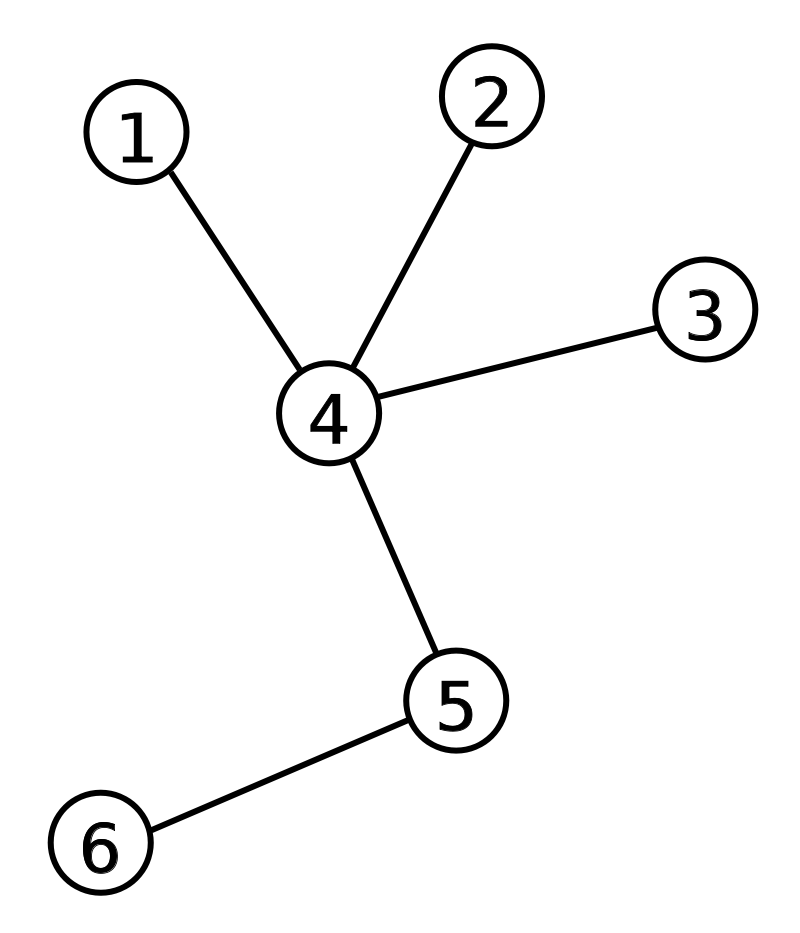
Kuo-chan wants to find the Prufer code of the given trees. Please help him.
Input
The first line contains a single integer n — the number of vertices.
Each of the next n - 1 lines contains two integer vi and ui — meaning there is an edge between vi and ui.
n <= 5000
1 <= vi, ui <= n
Output
The output should contains n - 2 distinct integers, meaning the Prufer code of the tree.
Remember to add new line in the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Kuo-chan is given a sequence A and a constant K as his birthday present from Yang-chan.
Kuo-chan is allowed to perfrom the following operation:
- push x — push x to the end of A
- pop — remove the median value of A (the median value of A is A[ (|A|+1)/2 ])
- programming tanoshi — for 1 <= i <= |A|, assign A[ i ] % K to A[ i ]
For example, if A = [4, 3, 5], K = 2
push 11 ► A = [4, 3, 5, 11]
pop ► A = [4, 5, 11]
pop ► A = [4, 11]
programming tanoshi ► A = [0, 1]
Yang-chan is curious about what A is after Kuo-chan performs some operations to it.
Help him find it out!
Input
The first line contains three integers N K Q — the length of A, the constant Yang-chan gives Kuo-chan, the number of operations Kuo-chan performs.
The second line contains N integers a1, a2, ..., aN (1 <= ai <= N) — the elements of A.
Each of the next Q lines describes the operations. Each line is one of three types:
- push x (1 <= x <= N)
- pop
- programming tanoshi
Different testcases have different constraints.
- N <= 103, Q <= N, K <= N, operations: {pop}
- N <= 103, Q <= 2N, K <= N, operations: {pop, push}
- N <= 103, Q <= 2N, K <= N, operations: {pop, push, programming tanoshi}
- N <= 105, Q <= N, K <= N, operations: {pop}
- N <= 105, Q <= 2N, K <= N, operations: {pop, push}
- N <= 105, Q <= 2N, K <= N, operations: {pop, push, programming tanoshi}
Output
You should print one line containing the elements of A after the operations. For 1 <= i <= |A|, the i-th number should be A[ i ].