| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13129 | prize! |
|
| 12719 | Binary search trees I: construction and traversal |
|
Description
There are n people, numbered 1 to n, in a circle and arranged in clockwise. They are playing a game, kth lucky people can get the prize.
The following are rules of the game:
1. Each prize has a lucky number.
2. Who count the lucky number can get a prize.
3. If the lucky number is odd, count clockwise.
4. If the lucky number is even, count counterclockwise.
5. The student that gets prize will leave the circle.
6. After someone leave the circle, if the new lucky number is odd, count from the next person, otherwise count from the previous person.
For example:
n = 8
m = 3
lucky number = 3 4 5
The sequence of getting prize is:
1 2 3
2 1 8 7
8 1 2 4 5
Then people 3, 5, 7 can get the prize.
Please use doubly circular linked list to solve this problem.
Input
The first line has two integer n and k, where n is the number of total people, and k is the number of prizes.
The second line has k positive number a1 ~ ak.
testcases:
1. 1 <= k <= n <= 10000, 1 <= ak <= n
2. 1 <= k <= n <= 10000, 1 <= ak <= n
3. 1 <= k <= n <= 10000, 1 <= ak <= n
4. 1 <= k <= n <= 1000000, 1 <= ak <= 10000000, n*k <= 300000000
5. 1 <= k <= n <= 1000000, 1 <= ak <= 10000000, n*k <= 300000000
6. 1 <= k <= n <= 1000000, 1 <= ak <= 10000000, n*k <= 300000000
Output
The output has k lines, each line contains a number: who can get the prize.
Sample Input Download
Sample Output Download
Partial Judge Code
13129.cPartial Judge Header
13129.hTags
Discuss
Description
This problem uses partial judge. Please select gcc compiler when submitting.
A binary search tree is a binary tree that has the following properties:
-
For any node, its key is greater than the keys stored in the left subtree.
-
For any node, its key is smaller than the keys stored in the right subtree.
-
For any node, the left subtree and the right subtree are binary search trees respectively as well.
-
Every node has a unique key. No two nodes share the same key.
For example, the two following trees are binary search trees.
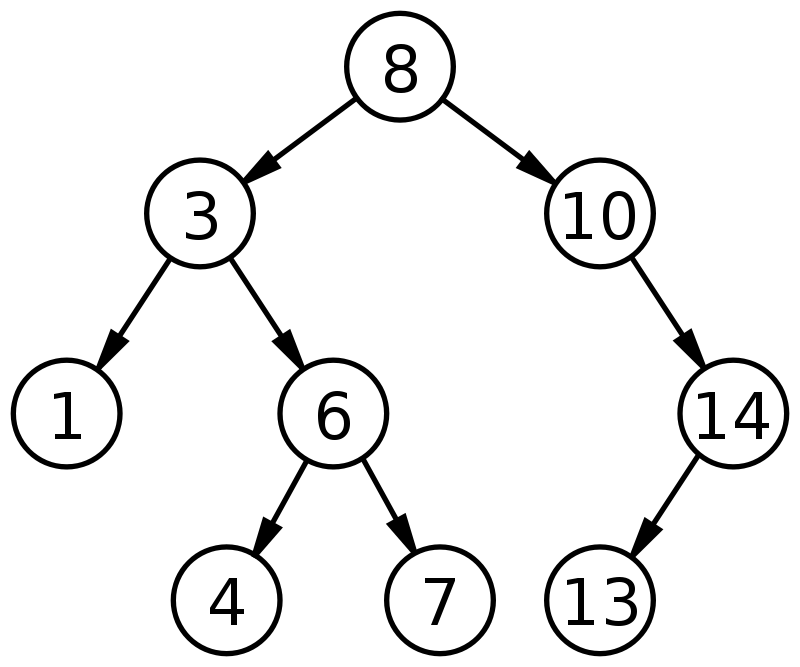
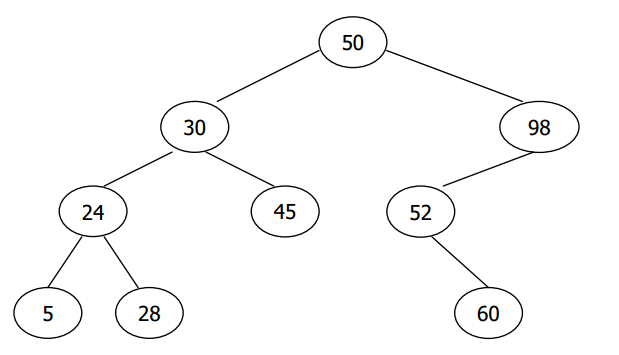
Given the pre-order traversal of a binary search tree, please output the in-order traversal and post-order traversal of the binary search tree. It can be proven that for no two binary search tree shares the same pre-order traversal.
Input
The first line is an integer T, meaning that there are T test cases in a single input file.
For each test case, the first line is an integer N, denoting the size of the binary search tree. The next line are N integers, denoting the pre-order traversal of the binary search tree.
-
1 <= T <= 2000
-
1 <= N <= 106
-
1 <= N x T <= 2 x 106
-
Be careful of memory leak
-
To pass all test cases, try to come up with an O(N) algorithm to build the binary search tree.
-
-
0 <= key of node <= 109
Output
For each test case, please output two lines: The first line is the in-order traversal of the binary search tree. The second line is the post-order traversal of the binary search tree.
Note that there is a space after each output number. e.g. use printf("%d ", var_to_be_printed) when printing.