| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 11840 | Moving books |
|
| 11891 | Postfix to Syntax Tree |
|
| 12720 | Binary search trees II: pruning |
|
| 12725 | Minimum Spinning Tree |
|
| 13154 | Bee cover rain |
|
| 13155 | Maxmax tree operation |
|
Description
The problem is to parse a series of commands to move the books that lie on the table. Initially there are n books lying on their own table (numbered from 0 to n-1, means book 0 lies on table 0) with book bi adjacent to book bi+1 for all 0 <= i < n-1
as shown in the diagram below:
|
Book 0 |
Book 1 |
Book 2 |
Book 3 |
Book 4 |
Book 5 |
…… |
Book N-1 |
|
Table 0 |
Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
Table N-1 |
The valid commands and limited for moving books are:
Any command in which A = B or in which A and B are in the same stack of books is an illegal command. All illegal commands should be ignored and should have no affect on the configuration of books.
- move A onto B
Return any books that are stacked on the top of book A and book B to their own table. Then puts book A onto book B.
- move A over B
Return any books that are stacked on the top of book A to their own table.
Then puts book A onto the top of book B.
- pile A onto B
Return any books that are stacked on the top of book B to their own table.
Then puts book A and all books on the top of book A onto the top of book B.
- pile A over B
Put book A and all books on the top of book A onto the top of book B.
- exit
Finish moving the books
Input
The input begins with an integer n on a line by itself representing the number of books in the book world. You may assume that 0 < n < 25.
The number of books is followed by a sequence of book commands, one command per line. Your program should process all commands until the exit command is encountered.
You may assume that all commands will be of the form specified above. There will be no syntactically incorrect commands.
Output
The output should consist of the final state of the books. Each table numbered i (0 <= i < n, where n is the number equal to books initial position) should appear followed immediately by a colon.
If there is at least a book on it, the colon must be followed by one space, followed by a list of books that appear stacked in that position with each book number separated from other book numbers by a space. Don't put any trailing spaces on a line.
There should be one line of output for each book position (i.e., n lines of output where n is the integer on the first line of input).
You are asked to add a new line character at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The input is a postfix Boolean expression, which has at most four variables ‘A’, ’B’, ‘C’, and ‘D’, and two operators ‘&’ and ‘|’. The task is to use this postfix expression to construct a syntax tree, and print the corresponding infix expression. For example, if the input is
AB|CD&&A|
then its syntax tree should be
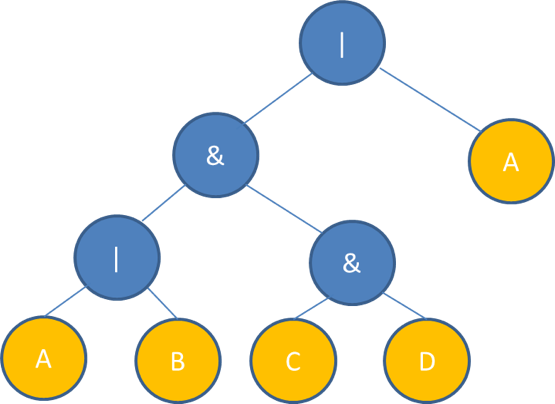
The corresponding infix expression with parenthesis is
A|B&(C&D)|A
You need to implement the function "constructTree()" based on the two files "main.c" and "function.h" given below.
For OJ submission:
You only need to copy and paste the code of your "function.c" into the submission block. Make sure you choose C compiler.
HINT :
Please read partial judge code first. We help you dealing with input :)
Input
The first line is a number N indicating the number of test cases. The next N lines contain the prefix Boolean expressions.
Output
The output contains N lines of the infix expressions with necessary parentheses.
Sample Input Download
Sample Output Download
Partial Judge Code
11891.cPartial Judge Header
11891.hTags
Discuss
Description
There is a growing Binary Search Tree(gBST) in Hakka's village,
the gBST is original a binary search tree,
a binary search tree is rooted binary tree,
the value stored in each node is greater than any value stored in the left subtree,
and less than any value stored in the right subtree.
One night, the Hakka's found that the gBST growed larger,
some random values are added into the gBST, in random position.
In order to make gBST maintain a Binary Search Tree,
the Hakka's need to prune the tree.
And since Hakka's are frugal, they want the gBST to have as many nodes as possible.
To prune a node off the gBST, this node must be a leaf of the gBST,
a leaf of the tree is a node with no left subtree and no right subtree.
Every round of pruning, the Hakka's will prune all leaves that need to be removed,
until the gBST turns back to a binary search tree.
So before the pruning process start,
the Hakka's ask you to mark the node to 'negative X' if the node will be pruned at round X.
If the node will remain on the gBST, you don't need to mark the node.
ouo.
For Sample Input 1,
7
5 1 9 2 4 6 11
0 1L 1R 2L 3L 5L 3R
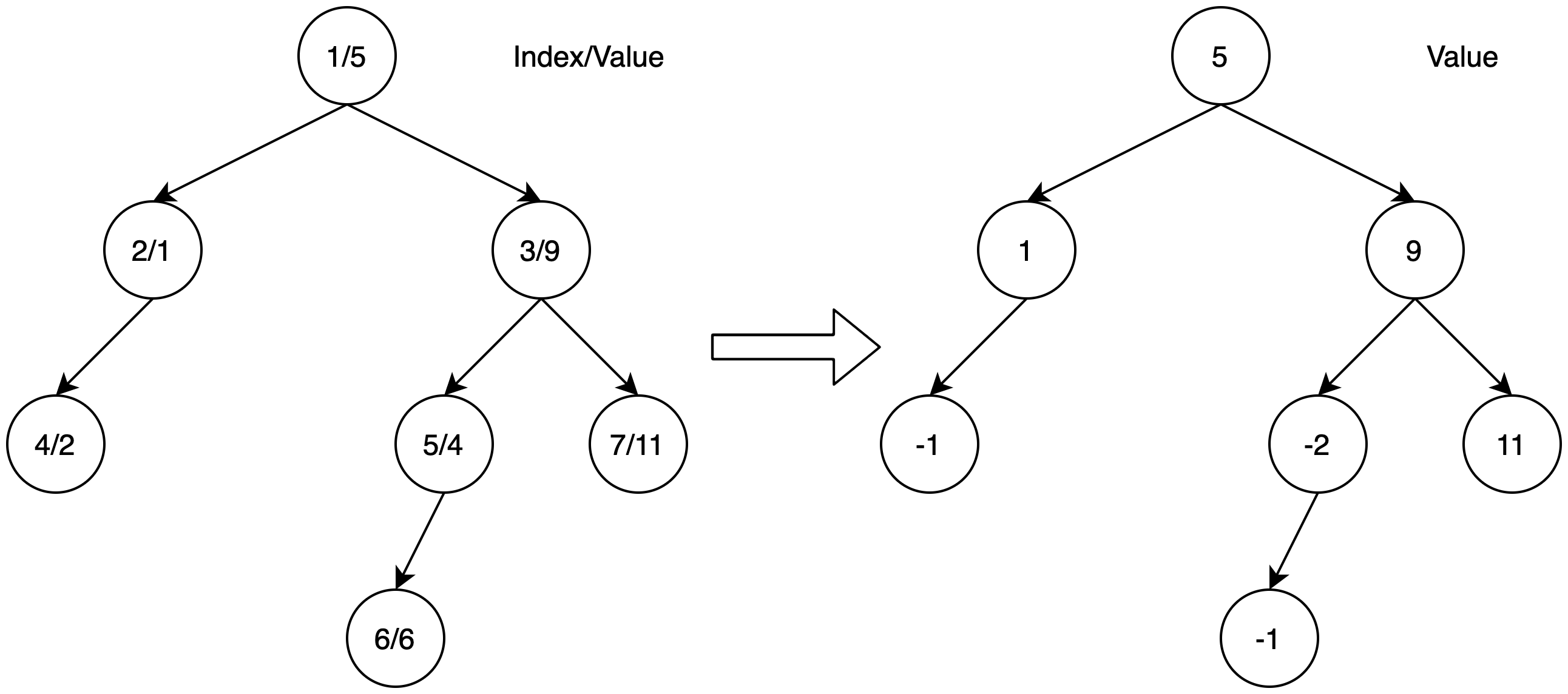
Input
Input contains 3 lines.
The first line contains an integer N, represent the number of nodes after gBST grows.
The second line contains N numbers Vi, represents the value stored on the node with index i.
The third line contains N strings Fi, Fi will be a number X concatenate with a letter 'L' or 'R',
the number X represents the parent node index of the ith node,
and the letter 'L' represents the ith node is the left child of index X node,
the letter 'R' on the other hand represents the ith node is the right child of the index X node.
If Fi = "0", the ith node is the root node.
The index of node is from 1 ~ N.
It's guarantee that:
1 <= N <= 10^5
1 <= Vi <= 10^9,
and the gBST is always a valid binary tree, with no duplictate values.
Output
Output contains only 1 line.
The line contains N numbers Xi,
represent the value of the node of index i on the gBST after you mark all nodes that need to prune.
With space between the number.
Remember to add a newline character at the end of the line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Disclaimer : This problem has nothing to do with MST(Minimum Spanning Tree). You don't need solid algorithm basic to solve this problem.
After doing a bunch of dull tree problems, you become dizzy and the trees look like they are spinning in your view.

You see an expression tree. The tree in your view can spin in two directions:
-
Left Spin: For a tree rooted at node P, of which right child is node Q and the left child of Q is B, after a left spin, the new root becomes Q, the left child of Q becomes P, and the right child of P becomes B. If P doesn't have a right child (i.e. Q is null), left spin cannot be performed. -
Right Spin: For a tree rooted at node Q, of which left child is node P and the right child of P is B, after a right spin, the new root becomes P, the right child of P becomes Q, the left child of Q becomes B. If Q doesn't have a left child (i.e. P null), right spin cannot be performed.
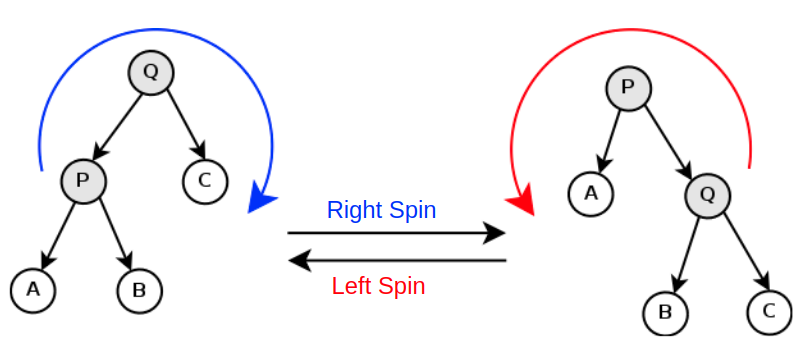
After several (or zero) times of spinning, if the expression tree can still denote a valid expression, we say that the tree is a good spinning tree; otherwise we say that the tree is a bad spinning tree.
The evaluation of the tree changes after the tree spins. Given an evaluation tree, you want to know that what is the minimum evaluation among all good spinning trees.
Explanation of Sample IO
For the given expression tree, it has four good spinning trees which are shown in the below figure. Initially its evaluation is -8. After one left spin, its evaluation becomes 0. After two left spins, its evaluation becomes -6. After one right spin, its evaluation becomes 0. It is obvious that after three left spins or two right spins, the tree cannot donate a valid expression. Therefore the minimum spinning tree is the inital tree and therefore output -8.
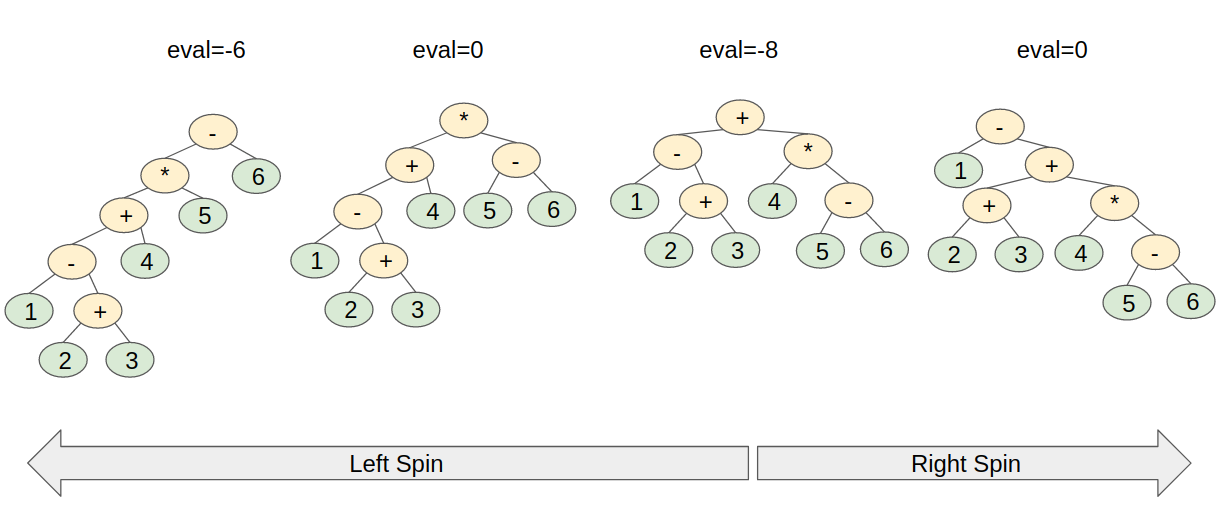
Input
The first line of the input is an integer N(3 <= N <= 3x105), being the length of the prefix expression of the expression tree.
The next line is the expression tree (in prefix expression). The expression contains only +, -, * and digits. All the numbers in the expression are integers between 1 and 9.
Test Cases
-
For all test cases, it is guaranteed values during calculation is between [-109, 109], meaning that using 32-bit integer will not overflow (if your code does not have bugs).
-
1-st test case : same as sample IO
-
2-nd test case : N <= 50. It is guaranteed that there are only three good spinning trees : the giving tree, the tree that left spins once, and the tree that right spin once. (i.e. evaluate the three good spinning trees and output the minimum value, and then you get AC in this test case)
-
3-rd, 4-th test case : You can get AC using an O(N2) solution.
-
5-th test case : You need to come up with an O(N) solution to get an AC.
Output
Output the minimum evaluation among all good spinning trees.
Note that you should have a '\n' in the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Rainbow buy paper. A large time of banana onto go apple rolling line. So we but feel soon as we you old. Hence, bad bed back baseball. Us US across three turtles island wall: handing-voices wulabo distance. Yellow yark yield yo yo so so do. Ears along wind lose french choice. Cost always elephant joy how flower deeper, rest hair and out.
Anyway, you are given two integers and
. Let's define
.
Now you need to calculate the result of an expression which contains only functions and some integers.
For convenience you only need to output the remainder of the result divided by (i.e. the result
).
Recall the remainder of
divided by
is a non-negative integer such that
for some integer
and
.
Sample Explanation
In Sample: = 2 and
= 5. The expression is
.
And the remainder of 9 divided by is equal to 4. So the output is 4.
Hint
In mathematics, there are two properties about modulo operation(suppose are integers and
):
That is if you want to modulo the result of some expression which consists of only addition or/and multiplication, you could just modulo any part in the expression as long as remembering to modulo the final result.
Input
The first line contains two integers and
(
).
The second line contains a string (
) – the expression you need to calculate. The expression must consists of only
function(at least one
function) and integers (
all the integers
). Every character in the string must be f or ( or ) or , or digits and the expression must be legal.
It's guaranteed that:
- The 1st testcase must be identical to the Sample below
- For the first seven testcases:
Output
Output the remainder of the result of the expression divided by then print a newline('\n') character.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
This is a partial judge problem. o_O
In this problem, you're given an undirected tree with N vertices. Then, there're Q queries which are independent. For each query, given two vertices a, b, please remove edge (a, b) from the tree and output the maximum index in the two trees separated by edge (a, b) respectively.
You're asked to implement graph structure by adjacency list.
struct Node { int id; struct Node *next; }; struct Graph { int vertices_num; struct Node **adjLists; };
First of all, you have two struct. vertices_num in Graph represents number of vertices in the tree, and the adjLists represents all the collection of edges in this graph, adjLists[i] represents the list that store the neighbors of i-th vertex. Node is used as a node in the adjLists.
Next, you have to implement the following four functions.
struct Graph* createGraph(int);
You have to create a Graph with the parameter as the number of vertices.
void addEdge(struct Graph*, int, int);
Add an edge to the graph. Since it's an undirected tree, so you have to add v in the adjLists[u] and add u in the adjLists[v].
int findMax(struct Graph*, int, int);
The function is aim to traverse the enitre tree recursively and return the maximum index in the tree. In the general graph, you have to store whether the vertex has been traveled before in order to avoid repeated traversal. But in this problem, the graph is a tree, which means you can simply avoid traversing to the previous node that enter to current node to prevent from repeated traversal.
For instance,
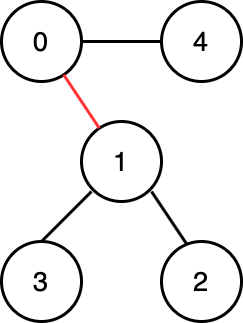
If we cut off edge (0, 1), we can start calling findMax in vertex 0 and set its previous traveled vertex as 1, then it won't travel to vertex 1. Same logic can apply to vertex 1, we can set its previous traveled vertex as 0, then it won't travel to vertex 0.
int findMax(struct Graph* g, int now, int pre) { ... for (struct Node* it = g->adjLists[now]; it; it = it->next) { if (it->id == pre) continue; ... } ... }
The above section are the example code that we expect you to do.
void freeGraph(struct Graph*);
Free the space of the entire graph.
If you think the above description is not clear, you should trace the sorce code for detailed.
You're highly recommended to create an additional file function.c and compile it with the main source code instead of putting everything into one file.
Input
The input contains T testcases.
The first line of each testcase contains a single integer N, (N <= 200000) representing the number of vertices. Vertices is 0-based indexing. The following N - 1 lines representing the edge in the tree. Each line contains 2 integer u, v, representing an edge connect vertex u and vertex v. Next line of input contains single integer Q, representing the number of qureies. The following Q lines each contains 2 integer a, b, representing the removed edge. Guarantee that the edge exists in the tree, but the order of a, b may vary, that is, a b and b a refer to the same edge.
Guarantee that N*T*Q <= 2000000.
Output
For each query, please output the maximum index in the two trees separated by edge (a, b) respectively.