| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 10990 | cheat sheet |
|
| 11366 | Moving the books |
|
| 13156 | Guess Left or Right |
|
| 13157 | Beef color vain |
|
Description
Linked list
typedef struct _Node {
int data;
struct _Node *next;
} Node;
/* print the content of the linked list.*/
void printList(Node *head)
{
Node *temp;
for(temp=head; temp!=NULL; temp=temp->next) {
printf("%d ", temp->data);
}
}
/*Insert a node after the node pointed by nd.
Return 1 if insertion succeeds.
Otherwise, return 0.*/
int insertNode(Node* nd, int data)
{
if (nd != NULL) {
Node* temp = (Node*)malloc(sizeof(Node));
temp->data = data;
temp->next = nd->next;
nd->next = temp;
return 1;
}
return 0;
}
/*Delete a node after the node pointed by nd.
Return 1 if insertion succeeds.
Otherwise, return 0.*/
int deleteNode(Node* nd)
{
if (nd != NULL) {
Node* temp = nd->next;
if (temp != NULL) {
nd -> next = temp->next;
free(temp);
return 1;
}
}
return 0;
}
Binary tree
typedef struct _node {
int data;
struct _node *left, *right;
} BTNode;
Tree traversal
- Pre-order: visit root, left subtree, and right subtree
- In-order: visit left subtree, root, and right subtree
- Post-order: visit left subtree, right subtree, and root
Expression order
- Prefix: operator, left operand,and right operand
- Infix: left operand, operator, and right operand
- Postfix: left operand, right operand, and operator
Syntax tree
The internal nodes are operators, and the leaves are operands.
Recursive evaluation of prefix expression
/*It is a pseudo code */
int evalBoolExpr(){
char c = getchar();
If c is an operator
op1 = evalBoolExpr();
op2 = evalBoolExpr();
return op1 c op2;
Else if c is a variable
return the value of c;
}
Grammar of infix expression with parenthesis
- EXPR = FACTOR| EXPR OP FACTOR
- FACTROR = ID | (EXPR)
/*Suppose expr[] is an array of expression and pos is the current position, which initially is strlen(expr)-1. */
/*-------------------------------------*/
BTNode* makeNode(char c)
{
int i;
BTNode *node = (BTNode*)malloc(sizeof(BTNode));
set node->data
node->left = NULL;
node->right = NULL;
return node;
}
/*-------------------------------------*/
BTNode* FACTOR()
{
char c;
BTNode *node = NULL;
if (pos>=0) {
c = expr[pos--];
if (c is an ID) {
node = makeNode(c);
} else if (c==‘)’) {
node = EXPR();
if(expr[pos--]!= '(') {
printf("Error!\n");
freeTree(node);
}
}
}
return node;
}
/*-------------------------------------*/
BTNode* EXPR()
{
char c;
BTNode *node = NULL, *right=NULL;
if (pos>=0) {
node = right = FACTOR();
if (pos>0) {
c = expr[pos];
if (c is an operator) {
node = makeNode(c);
node->right = right;
pos--;
node->left = EXPR();
}
}
}
return node;
}
Input
Output
Sample Input Download
Sample Output Download
Tags
Discuss
Description
The problem is to parse a series of commands to move the books that lie on the table. Initially there are n books lying on their own table (numbered from 0 to n-1, means book 0 lies on table 0) with book bi adjacent to book bi+1 for all 0 <= i < n-1
as shown in the diagram below:
|
Book 0 |
Book 1 |
Book 2 |
Book 3 |
Book 4 |
Book 5 |
…… |
Book N-1 |
|
Table 0 |
Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
Table N-1 |
The valid commands and limited for moving books are:
Any command in which A = B or in which A and B are in the same stack of books is an illegal command. All illegal commands should be ignored and should have no affect on the configuration of books.
1. pile A onto B
Return any books that are stacked on the top of book B to their own table.
Then puts book A and all books on the top of book A onto the top of book B.
2. exit
Finish moving the books
Hint: you can use following code.
#include <stdio.h>
#include <stdlib.h>
typedef struct _Node{
int val;
struct _Node* next;
} Node;
Node* table[25];
int position[25];
void resetBook(int p2) {
}
void pileOnto(int p1, int p2) {
}
void initialize(int n) {
}
int main() {
int n;
int i;
scanf("%d", &n);
initialize(n);
while(1){
char input[100] = {0};
int p1, p2;
scanf("%s", input);
if(input[0] == 'e')
break;
scanf("%d", &p1);
scanf("%s", input);
scanf("%d", &p2);
if(position[p1] == position[p2])
continue;
resetBook(p2);
pileOnto(p1, p2);
}
Node* tmp;
for(i = 0; i < n; i++){
printf("%d:", i);
tmp = table[i]->next;
while(tmp != NULL){
printf(" %d", tmp->val);
tmp = tmp->next;
}
printf("\n");
}
return 0;
}
Input
The input begins with an integer n on a line by itself representing the number of books in the book world. You may assume that 0 < n < 25.
The number of books is followed by a sequence of book commands, one command per line. Your program should process all commands until the exit command is encountered.
You may assume that all commands will be of the form specified above. There will be no syntactically incorrect commands.
Output
The output should consist of the final state of the books. Each table numbered i (0 <= i < n, where n is the number equal to books initial position) should appear followed immediately by a colon.
If there is at least a book on it, the colon must be followed by one space, followed by a list of books that appear stacked in that position with each book number separated from other book numbers by a space. Don't put any trailing spaces on a line.
There should be one line of output for each book position (i.e., n lines of output where n is the integer on the first line of input).
You are asked to add a new line character at the end.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Today is your birthday, your father wants to prepare a gift for you. He ranks his brains and finally decide what to give. Since you are a college student major in computer science, he gives you a rooted binary tree for your birthday! But at the time you are unpacking the gift, you accidentally damage the binary tree! What a pity! You have tried very hard to restore the information of the binary tree but end up failure. For each node, you know which two nodes are its children, but you don't know which one is left child and which one is right child.
Fortunately, There's an inorder traversal sequence of the binary tree on the package, and you want to know whether the broken information of the binary tree is possible to form the inorder traversal sequence on the package.
Note:
The following figure is the way to form the tree that meets the input of sample testcase 1 and its inorder traversal is identical to the input inorder traversal.
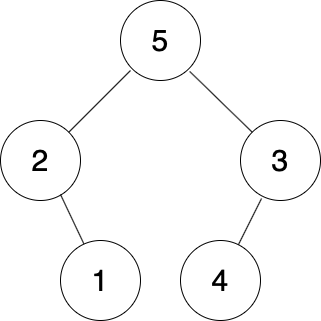
Input
The input contains T testcases.
The first line of each testcase contains a single integer N representing the number of node in the binary tree. The index of nodes in the binary tree is 1-based.
For the following N lines, each line contains two integers. For i-th line, the two integers represent the children of i-th node. 0 represents that the node doesn't exist.
Next line of the input contains N integers representing the inorder traversal sequence.
Constraint of testcases:
Testcase 1: N <= 5, T <= 4.
Testcase 2: T = 20, N <= 15, and node 1 is guarantee to be the root of the binary tree.
Testcase 3: T = 20, N <= 2000, and node 1 is guarantee to be the root of the binary tree.
Testcase 4: N * T <= 4 * 106, N <= 2 * 105, and node 1 is guarantee to be the root of the binary tree.
Testcase 5: T = 20, N <= 15.
Testcase 6: T = 20, N <= 2000.
Testcaes 7: T = 20000, N <= 10.
Testcase 8 ~ 10: N * T <= 4 * 106, N <= 2 * 105.
Output
For each testcase, if there exists a way to distribute nodes to left child or right child that its inorder traversal is identical to the input inorder traversal, then output "YES" otherwise "NO".
Remember to add a newline character at the end of every line.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
Vainglory bu...... Anyway you are given two integers and
. Let's define
.
Also you are given a sequence and an expression which contains only
functions and some elements of
like
or
(supposing
).
Now you need to execute operations. In the
-th operation, you are given two integers
and
. First you have to change
into
. Then output the result of the expression.
For convenience, you only need to output the remainder of the result divided by (i.e. the result
) in each operation.
Recall the remainder of
divided by
is a non-negative integer such that
for some integer
and
.
Sample #2 Explanation
In Sample #2: and
. Sequence
is
. The expression is
.
In the 1st operation: and
. So after changing
into
, sequence
becomes
(still the same). So the expression
. The remainder of 181 divided by
is equal to 1.
In the 2nd operation: and
. So after changing
into
, sequence
becomes
. So the expression
. The remainder of 181 divided by
is equal to 1.
In the 3rd operation: and
. So after changing
into
, sequence
becomes
. So the expression
. The remainder of 229 divided by
is equal to 9.
Hint 1
In mathematics, there are two properties about modulo operation(suppose are integers and
):
That is if you want to modulo the result of some expression which consists of only addition or/and multiplication, you could just modulo any part in the expression as long as remembering to modulo the final result.
Hint 2
In mathematics, is equal to
rather than
.
But if you execute printf("%d\n", -4 % 3) in C, you will get -1 rather than 2.
That's because C only guarantees (a / b) * b + a % b is equal to a (i.e. ). That is a % b is equal to a - (a / b) * b. That's why you will get -1 rather than 2 in above case. Try yourself to fix this issue, if necessary.
Input
The first line contains two integers and
(
).
The second line contains a integer (
) – the number of elements in the sequence
.
The third line contains integers
(
) – all the elements in the sequence
.
The fourth line contains a string (
) – the expression you are given. The expression must consists of only
function (at least one
function) and integers which are the indexes corresponding to the elements of
(
all the integers
). Every character in the string must be f or ( or ) or , or digits and the expression must be legal.
The fifth line contains a integer (
) – the number of times you need to execute operations.
Then lines follow. Each line contains two integers
and
(
) – the content of each operation.
It's guaranteed that:
- The 1st testcase must be identical to the Sample #1 below
- For the first 5 testcases:
- For the first 7 testcases:
Output
For each operation, output the remainder of the result divided by then print a newline('\n') character.
Note: there are two sample below. "# Sample Input 1/2" and "# Sample Output 1/2" are not the part of input and output.
They are just for marking that the following content corresponds to which sample.