| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 13232 | Closest Pair of Points (Simple Version) |
|
Description
You are given 2n points on the plane, where n of them lie on the x-axis and another n of them lie on the y-axis. Additionally, the given points will never appear at the origin (point (0, 0)). Your task is to pair the points on x-axis and y-axis one by one to minimize the sum among the distance between the pairing points.
Formally, given a set of n points X = {(x1, 0), (x2, 0), …, (xn, 0)} and a set of n points Y = {(0, y1), (0, y2), …, (0, yn)}, calculate the weight sum of the minimum weight matching for bipartite G = (V, w), where V = X ∪Y and w: X×Y → R is the Euclidean distance between x ∈ X and y ∈ Y. (You can skip this paragraph if you are not familiar with the concepts.)
In this problem, each test case contains multiple cases. Each case is independent. You need to output one answer per each case. Also, there is no implementation constraints in this problem (built-in sorting fuctions or containers are allowed).
Input
The first line contains an integer T, representing the number of cases.
The first line of each case contains a singe integer n, representing the number of pairs you need to find.
The next 2n lines contains two integers x and y, representing the coordinates of the points.
It is guaranteed that:
- No point is at the origin.
- n points are on the x-axis, and the other n points are on the y-axis
- 1 ≤ T ≤ 100
- -108 ≤ x, y ≤ 108
- 1 ≤ n ≤ 105
- The sum of n among all cases ≤ 105
Output
For each case, output a single real number in 8 digit precision with a new line symbol, representing the value of the minimum sum among the distance between the pairing points (the weight sum of the minimum weight matching).
You can use the following template to output real number in 8 digit precision.
// Make sure you include the libraries below
#include <iostream>
#include <iomanip>
int main() {
// add this line of code at the beginning of you main function
std::cout << std::fixed << std::setprecision(8);
// Implement your code below
}
Sample input and Output Explanation
Sample Input 1
The given four points are shown below.
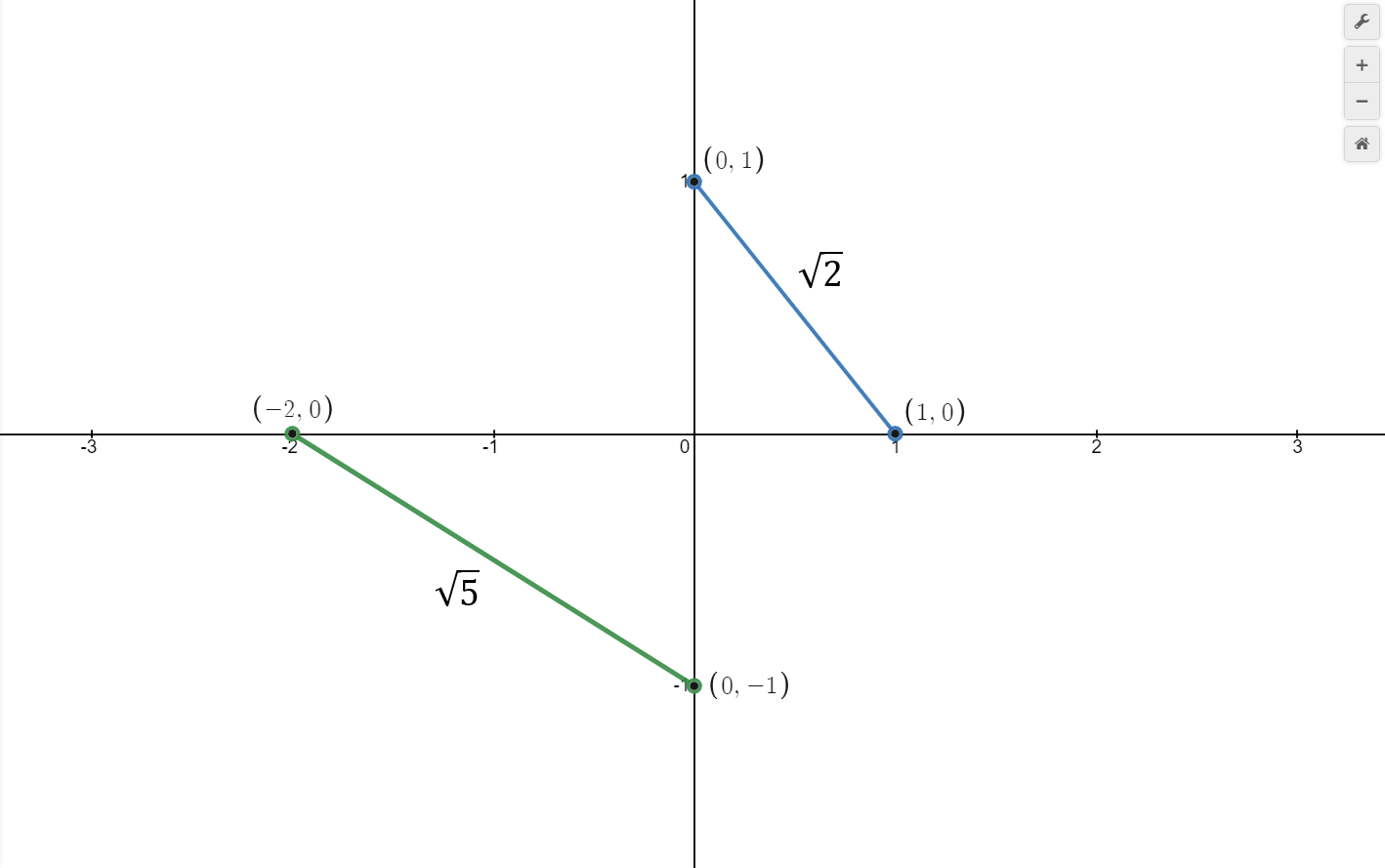
The pairing results are shown below. The output should be 20.5 + 50.5 ≈ 3.65028154 (8 digit precision)