| # | Problem | Pass Rate (passed user / total user) |
|---|---|---|
| 12146 | Too Many Things to Buy |
|
| 12254 | Thanos' Dilemma |
|
| 12662 | I got a perfect body |
|
Description
Ovuvuevuevue Enyetuenwuevue Ugbemugbem Osas is a shopaholic.
There are n different items in a store and Osas wants to buy every of them.
The i-th item cost ai dollars, but the price fluctuates greatly recently.
Tomorrow the i-th item's price will be bi dollars. Osas has an special ability that he can know the price tomorrow.
Because he's a shopaholic, he wants to buy every items in at most two days. Osas must buy at least k item at first day, or he will be crazy.
Help Osas find out the minimum money he should pay to buy every kinds of item in the shop.
Input
Input contains third lines.
First line contains two integer n ( 1 <= n <= 105 ) and k ( 0 <= k <= n ).
Second line contains n integer a1 ~ an ( 1 <= ai <= 105).
Third line contains n integer b1 ~ bn ( 1 <= bi <= 105 ).
Output
Output only contains one integer -- the minimum price Osas needs to pay.
remember to print \n at the end of output.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
In "Avengers 3", we know that Thanos wants to eliminate half of the world to keep the world in a good balance. But, have you ever wondered about how he choose "1/2" ? Why don't he choose "1/3", "1/4", or "253/502" ?
He knows that the population of this world would just keep growing, so he calculated the formula of population of this world:
On the i-th year from the start of the world, the population of this world P(i) would be: P(i-1) + 2 * P(i-2) + P(i-3).
From this formula, he concluded that P(1)=1, P(2)=12, P(3)=13.
According to this formula, he could estimate the populations of the world on every year, so that he could choose the percentage of the population he would like to eliminate. (We don't know how he choose)
Because Thanos has a lot of planets to conquer, he asks you to calculate P(x), while x is given by him.
The world has lived for so many years, so he might ask you P(x) where x would be very large. And in case of P(x) is super large, the number should mod 109+7.

"Thanos Thinking About This Problem"
If you click on this picture, something might happen...
- Given t, indicates the number of testcases.
- P(i) = P(i-1) + 2*P(i-2) + P(i-3)
- P(1)=1, P(2)=12, P(3)=13
- Given x, you are going to calculate P(x)%(109+7) of every testcase.
Hint: use fpw(快速冪) to solve this problem!
If we rewrite the equation into matrix form, we could get the following formula:
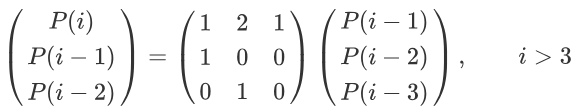
With this formula, we can do something more:
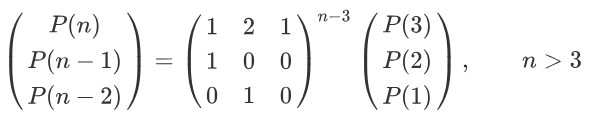
Now, we can implement fpw(快速冪) method on the matrix power part. For those n<=3, just output the answer.
Note that you are encouraged to implement a "matrix" struct to solve this easier.
Input
The first line contains one integer t, indicates the number of testcases.
There are t lines below, each line contains one integer x.
1 <= t <= 20, 1 <= x <= 1018.
Output
For each testcase, output exactly one integer P(x)%(109+7).
Remember to output a '\n' at the end of every testcase.
Sample Input Download
Sample Output Download
Tags
Discuss
Description
I got a young body.
~by anonymous coroner
You are a coroner, and you need to buy some Formalin to keep your body in good condition. There're n kinds of Formalin, and you have p dollars. Luckily the Formalin is on sale. If you buy exactly k kinds of Formalin, you only need to pay the most expensive one of them.
You got n products and p dollars.
Everytime you buy exactly k products at once, you only need to pay the most expensive product among the k products.
For the i-th product, the price equals to ai.
Find the maximum number of products you can buy with p dollars.
Example:
If n=5 and you got p=6 dollars.
If you buy exactly k=2 products, you only need to pay the most expensive one of them.
Products' price: 2, 4, 3, 5, 7.
In this case, you can buy products of price 4, 3 then you only need to pay 4 dollars.
You left with 2 dollars, then you can buy products of price 2.
The maximum number of products you can buy in this case is 3.

Input
The input start with t(1<= t <=10) means number of testcases.
Each testcase contains two lines.
First line contains three numbers n(2<=n<=3*10^5), p(1<= p <= 10^9), k(2 <= k <= n).
Second line contains n integer ai(1 <= ai <= 10000).
Output
For each testcase print the maximum number of products you can buy with p dollars.
Remember to print \n at the end of each output.