Description
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
ref: https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
video: https://youtu.be/qYo8BVxtoH4
We only implement the insertion, search, and some traversal methods of BST. Completing two existed classes Node and BinarySearchTree.
Node
Public Variables:
- data(int) int data stored in a node.
- left(Node*) pointer points to the left child node.
- right(Node*) pointer points to the right child node.
- parent(Node*) pointer points to the parent node.
Constructors:
- Node(int d) – Should initalize the data (data) store in a node to d, and initialize left, right and parent pointer to nullptr.
BinarySearchTree:
Public Variables:
- root(Node*) should point to the root element of the BST.
note: the root element is the first element inserted in the BST.
Constructors:
- The default constructor – Should initialize root to nullptr.
Public Methods:
- void Insert(int i) – Should create a Node(i), and insert it into the BST. Shown as below figure.
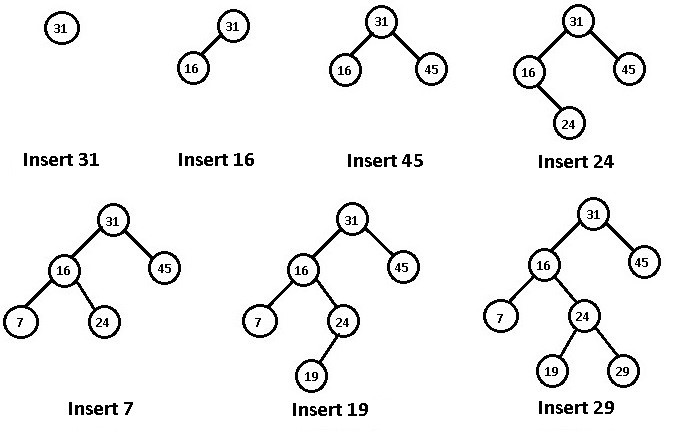
- Node* FindNode(int i) – Return the address of the node which data is equal to i. If can’t find any, return nullptr.
- Node* FindMinNode(Node *r) – Return the address of the node which data is the minimum in BST. If BST is empty, return nullptr.
- Node* FindMaxNode(Node *r) – Return the address of the node which data is the maximum in BST. If BST is empty, return nullptr.
- void LevelOrderTraversal(Node* r) – Traverse each level of the tree from the root downward, and at each level from left to right. Print all the node’s data stored in BST in order.
note: each two data is separated by a return value. Print ”/* empty */” if the BST is empty (root == nullptr).
For Example:
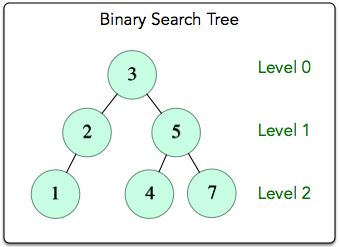
The level-order traversal is: 3->2->5->1->4->7.
hint: Queue or Vector is helpful for this implementation.
ref: https://www.hackerrank.com/challenges/30-binary-trees/problem?h_r=internal-search
/* You Don’t Need to Implement the Below Method */
- void InOrderTraversal() – Print all the node’s data stored in BST in order (LNR). If the list is empty print ”/* empty */”.
note: if insertion is implmented correctly, it will automatically print the data in ascending order. Also, you may use this function to check and debug.
Input
There are six kinds of input command.
insert i – Call Insert(i).
find i – Call FindNode(i).
min – Call FindMinNode(root).
max – Call FindMaxNode(root).
print – Call InOrderTraversal(root).
level – Call LevelOrderTraversal(root).
Output
No need to handle output. Check main.cpp for more details.