Description

This is a partial judge problem OwO

Finally, Spongebob and Patrick have successfully escaped from the police capture. So it’s unnecessary for Patrick to cosplay as a ninja, aka Patruto. (To know what happened before, you can refer to 12884 - Patruto and Spongebob run away.)

In order to enjoy their life of leisure, they decided to go catch some jellyfish for fun. But due to their poor reading ability, they eventually go to the "JerryFish" Field.

After arriving the JerryFish Field, they observed that some JerryFish would form a circle. And they always move regularly: two groups of consecutive JerryFish would exchange their position without messing up the order inside a group.

Now you need to help Spongebob and Patrick record the information of JerryFish circle. Formally there are N JerryFish. For convenience, we always number all the JerryFish from 1 to N in clockwise order. In the beginning, we know the beautiful value of the i-th JerryFish is v_i.
Then there are Q events. In the i-th event, two groups of consecutive JerryFish would exchange their position. And the number of JerryFish of these two groups is len_i. One group is the len_i consecutive JerryFish which start from the a_i-th JerryFish(in clockwise order). Another group is the len_i consecutive JerryFish which start from the b_i-th JerryFish(in clockwise order). They will exchange their position simultaneously. Note we always number all the JerryFish from 1 to N in clockwise order. So after one event, you may need to re-number all the JerryFish.

In the end, tell Spongebob and Patrick the beautiful value of all the JerryFish (in clockwise order).

Sample Explanation

Let's take Sample as an example. In Sample, N = 6 and Q = 3.

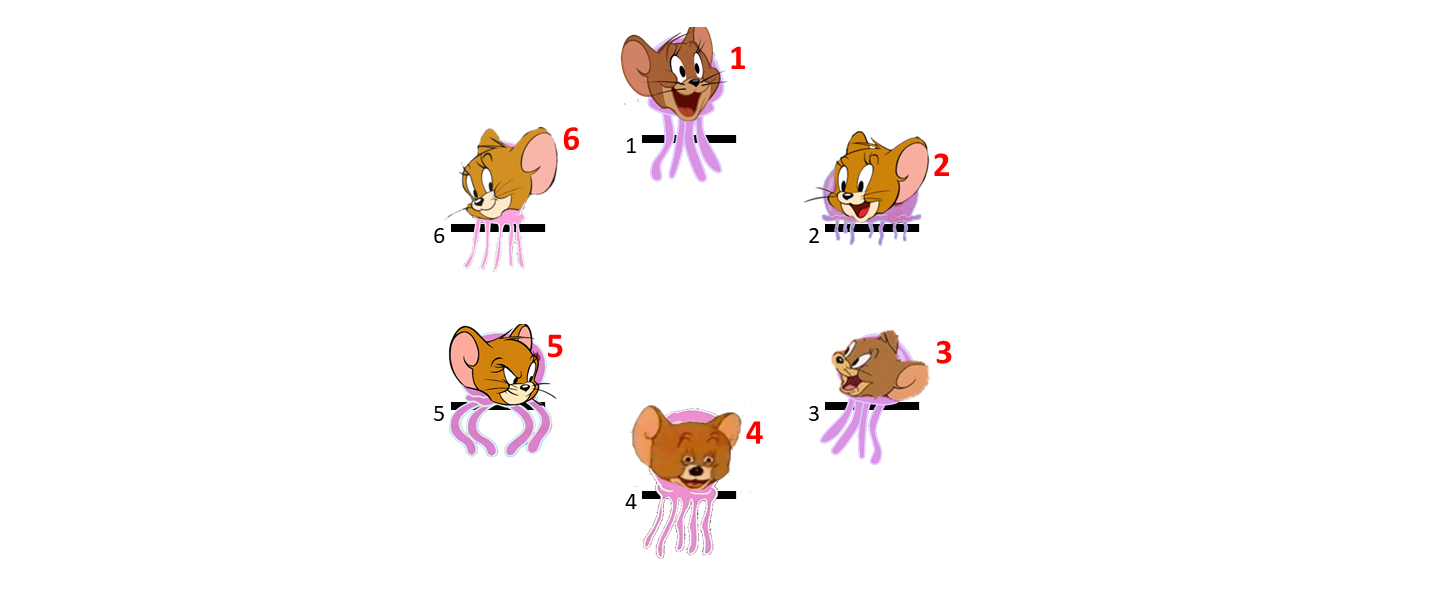
The first event: the 2nd JerryFish exchange its postion with the 4th JerryFish.

 

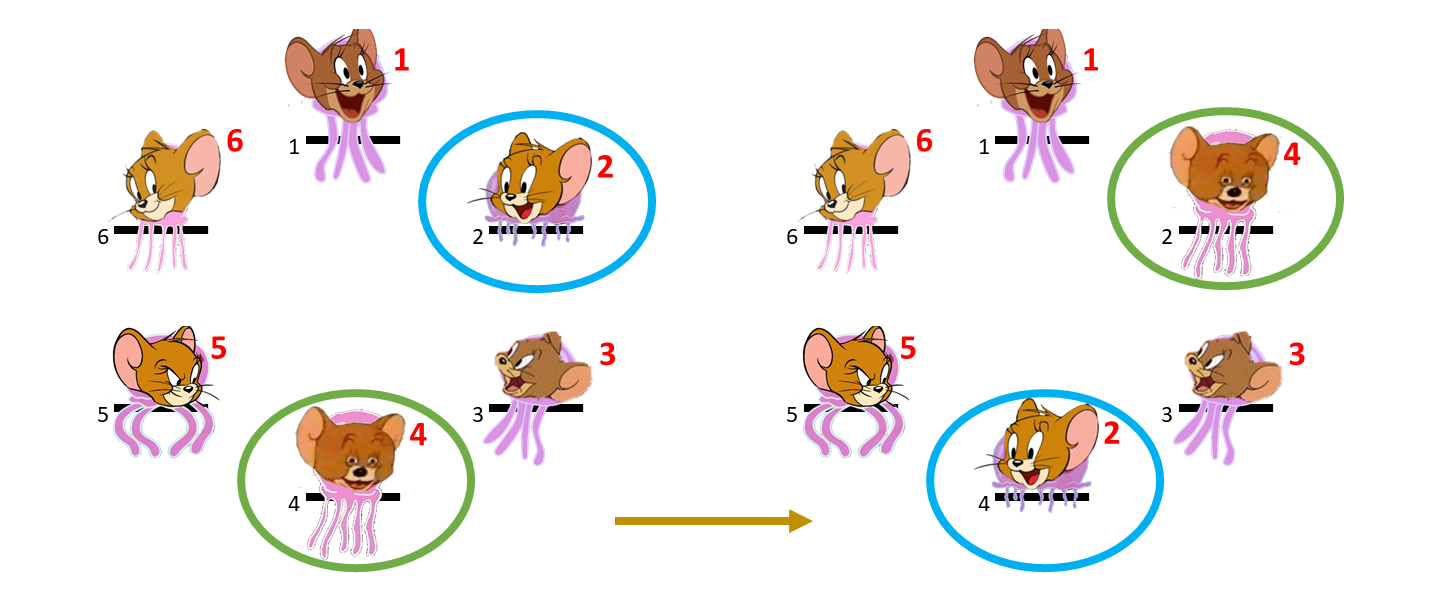
The second event: the 1st and the 2nd JerryFish exchange their postion with the 5th and the 6th JerryFish.

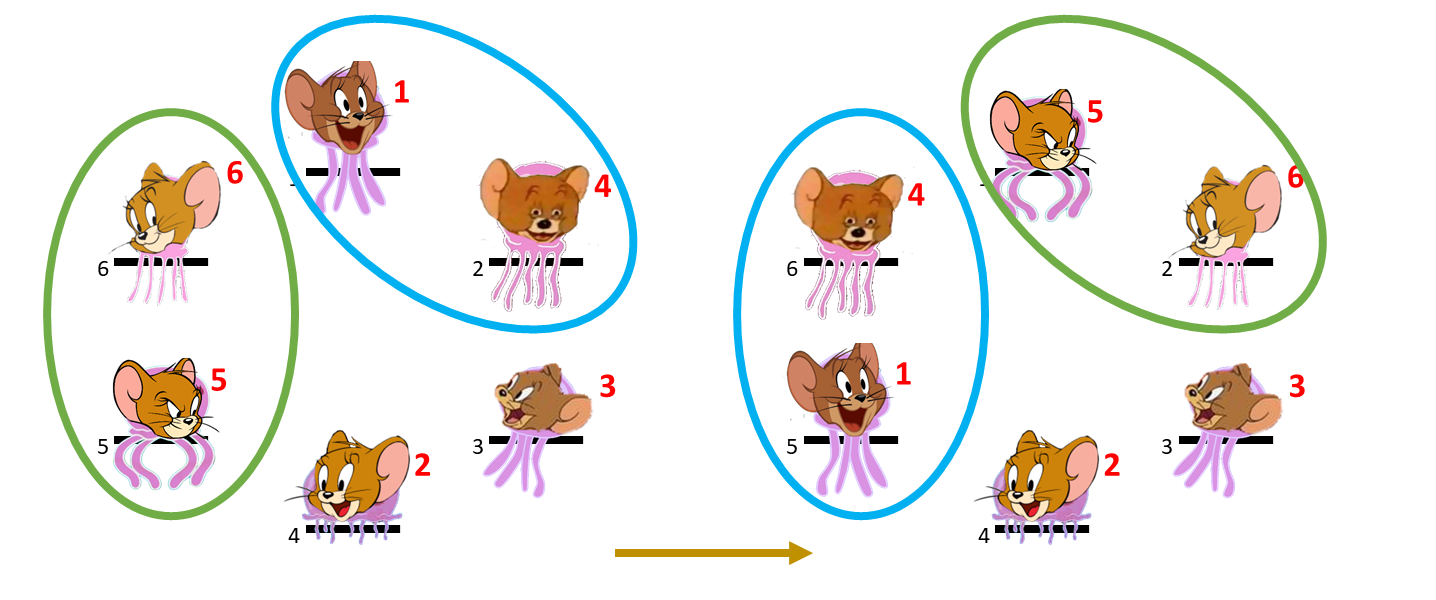
The third event: the 6th and the 1st JerryFish exchange their postion with the 3rd and the 4th JerryFish.

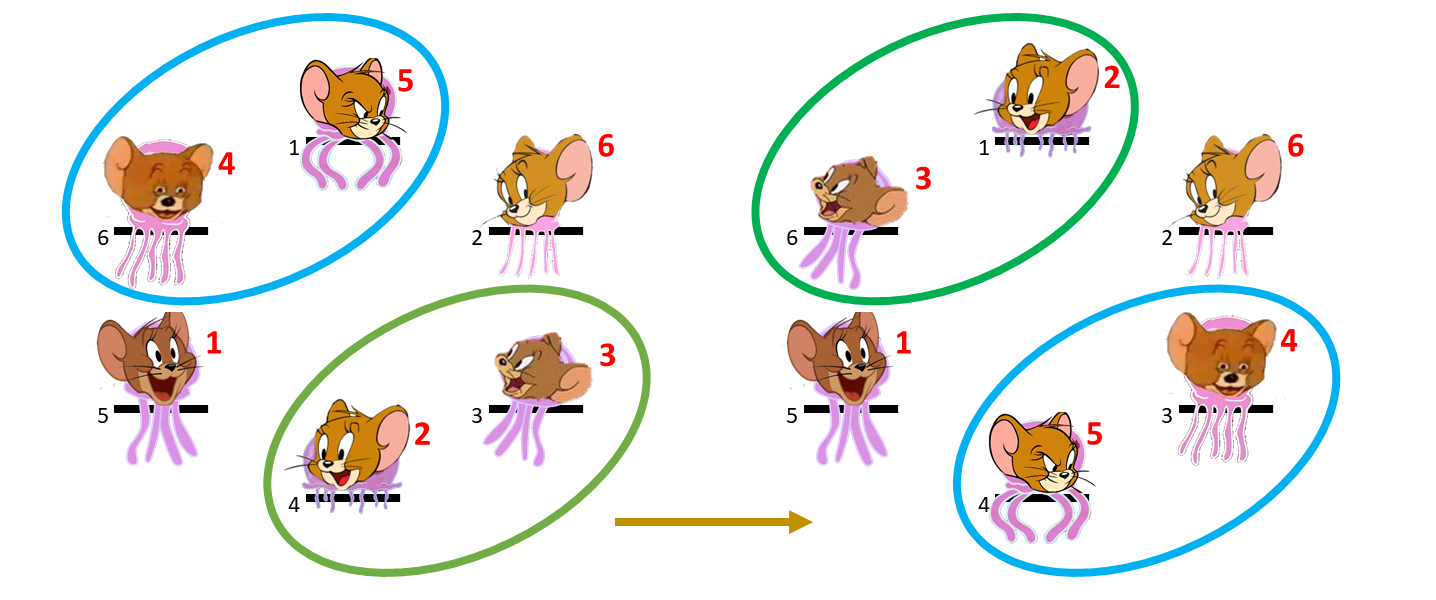
Finally the beautiful value of all the JerryFish are: 2 6 4 5 1 3.

Partial Code

Let's solve this problem with a circular linked list.

main.c

#include <stdio.h>
#include "function.h"
#define MAXN 100005
int arr[MAXN];
int main() {
    int N;
    scanf("%d", &N);
    for(int i=1;i<=N;i++)
        scanf("%d", &arr[i]);

    Node *head = NULL;
    createLinkedList(&head, N, arr);

    int Q;
    scanf("%d", &Q);
    for(int i=1;i<=Q;i++) {
        int a,b,len;
        scanf("%d %d %d", &a, &b, &len);
        swapTwoSegment(&head, a, b, len);
    }

    for(int i=1;i<=N;i++) {
        if(i > 1)    printf(" ");
        printf("%d", head->val);
        head = head->next;
    }
    printf("\n");
    return 0;
}

function.h

typedef struct node {
    struct node* next;
    int val;
} Node;
void createLinkedList(Node **head, int N, int *arr);
void swapTwoSegment(Node **head, int a, int b, int len);

You need to implement the two functions: createLinkedList and swapTwoSegment.

Input

The first line contains one integer N (2 ≤ N ≤ 10⁵) – the number of JerryFish.

The second line contains N integers v₁, v₂, ..., v_N (1 ≤ v_i ≤ N) – the beautiful value of each JerryFish.

The third line contains one integer Q (1 ≤ Q ≤ 100) – the number of events.

Then Q lines follow. The i+3-th line contains three integer a_i, b_i and len_i (1 ≤ a_i, b_i ≤ N, 1 ≤ 2 x len_i ≤ N) – the number of the starting JerryFish of two groups and the number of JerryFish in these two groups. It's guaranteed that there must not be such a JerryFish which is in the two groups simultaneously in each event.

 

It's guaranteed that:

• The 1st testcase must be identical to the Sample below

Output

After all the events output the beautiful value of all the JerryFish(in clockwise order).

Sample Input  Download

Sample Output  Download

Partial Judge Code

13133.c

Partial Judge Header

13133.h

Tags

Add Tag

Discuss