Description

You are given a tree of n nodes. Each of the n−1 edges of the tree is given by either '1' or '0'. 

Then you need to answer q questions. 
Each question has two integers k, m and a sequence of k nodes, a₁,a₂,…,a_k. Let's call a sequence [a₁,a₂,…,a_k] "good" if it satisfies the following criterion:

1. We will walk a path (possibly visiting same edge/node multiple times) on the tree, starting from a₁ and ending at a_k.
2. Start at a₁, then go to a₂ using the shortest path between a₁ and a₂, then go to a₃ in a similar way, and so on, until you travel the shortest path between a_k−1 and a_k.
3. If you walked over at least m '1' edge (marked by '1') during this process, then the sequence is 'good'.

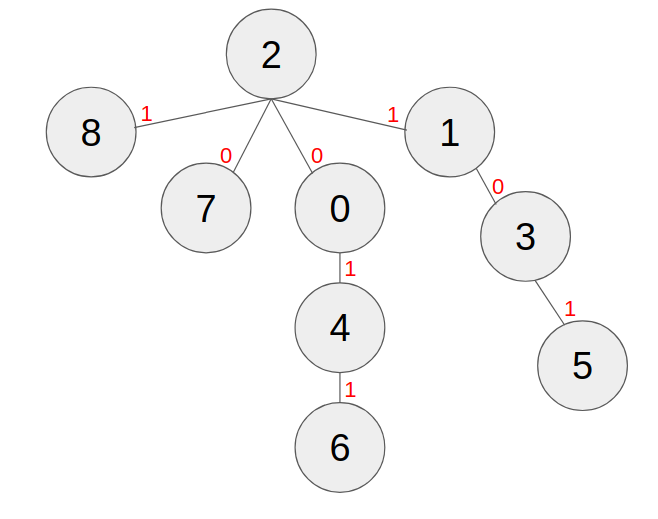
Consider the tree in the above figure. If m = 3, the following sequences are good: [8, 5], [8, 2, 6], [6, 0, 7, 8]. The following sequences are not good: [8, 0, 7], [3, 0, 7, 3], [8, 7, 0, 3].

 

Hint (You can jump to the Input/Output description first, and come back for hints if necessary): 

1. The shortest path is unique.

2. In addition to a linked list, another approch is to use three 2D array to store the tree to save computational time. 

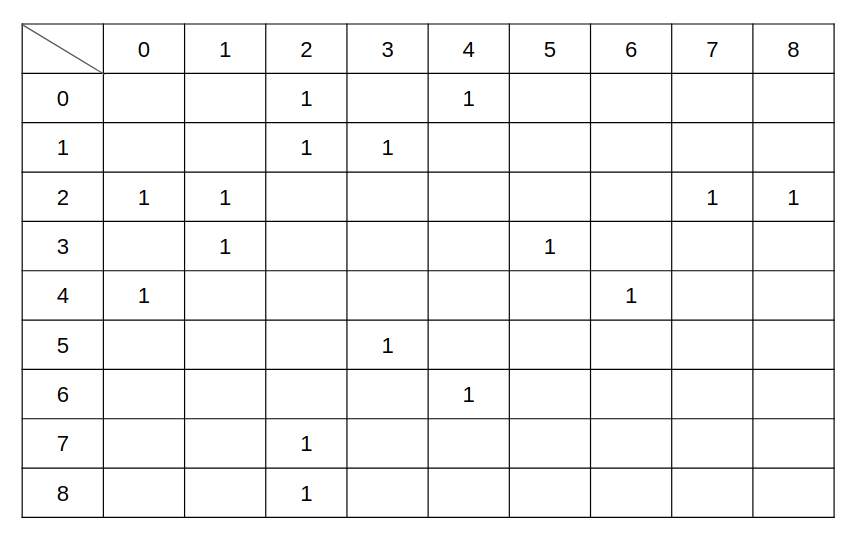
• edge[i][j] = 1 means there is an edge between a_i and a_j.
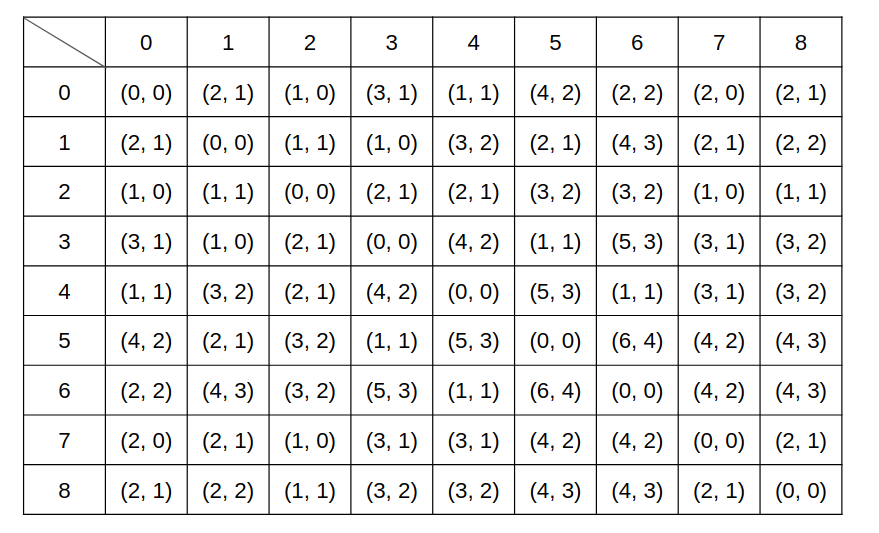
• path[i][j] means the distance between a_i and a_j.
• oneedge[i][j] means the number of '1' edge between a_i and a_j.

3. If there is an edge between a_i and a_k, and another edge between a_k and a_j, then the distance between a_i and a_j is 2, and you can count the number of '1' edge at same time.

Use the tree above as an example:

The edge array will look like:

The (path & oneedge array) will look like:

 

Input

The first line contains two integers n and q, the size of the tree and the number of questions, respectively.

Each of the next n−1 lines contains three integers u_i, v_i and x_i (1 ≤ u_i,v_i ≤ n, x_i ∈ {0,1}), where u_i and v_i denote the endpoints of the corresponding edge and x_i denotes the edge is '0' or '1' .

Each of the next q lines contains k + 2 integers, k, m, and a sequence of k nodes.

testcase:

(1/6) 2 <= n <= 100, 1 <= q <= 100, k = 100, x_i = 0

(3/6) 2 <= n <= 100, 1 <= q <= 100, k = 10

(2/6) 2 <= n <= 500, 1 <= q <= 1000, 2 <= k <= 10000

Output

The output has q lines, if the sequence is good, output YES, otherwise output NO.

Sample Input  Download

Sample Output  Download

Tags

Add Tag

Discuss