Description
In this problem, you are asked to implement a more efficient string matching method, called "rolling hash". In this method, strings are first mapped to integer hash values. Then, when two strings can be mapped to the same hash value, the two strings are said to be "matched".
The "rolling hash" maps a given string to an integer using the following function:
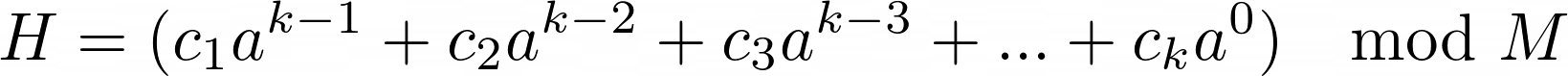 ,
,
where a=9487 is a constant and c1, c2, ..., ck are the chars of the given string.
Note that, the H hash value can be very large, so please use long long int type and module it by M=99999989 (the largest 8-digit prime number) in each add or multiply operation.
For example:
H("abc")=((((9487*9487)%M*'a')%M+(9487*'b')%M)%M+'c')%M=31238175
H("123")=((((9487*9487)%M*'1')%M+(9487*'2')%M)%M+'3')%M=10630166
Thus, "abc" is mapped to 31238175, while "123" to 10630166.
(It is guaranteed that in the test cases, no two different strings will be mapped to the same hash value if you follow the suggested hash function implementation.)
For complete problem description, please refer to 13277.
Given a set of strings S1 and another set of some query strings S2. In this problem, based on the "rolling hash" method, for each string in S2, you need to determine whether it exists in set S1 or not.
Hint.
- Suggested procedure to solve this problem:
- For each string of S1:
- convert the string into its hash value and store the value in an array.
- For each string of S2:
- convert the string into its hash value and search for the hash value in the array you created.
- Partial code for your reference:
-
#define a 9487
-
#define mod 99999989
-
-
long long int hash(char s[]) {
-
int len = strlen(s);
-
int i;
-
long long int ret = 0;
-
-
for (i = 0; i < len; i++) {
-
ret = (ret * a % mod + s[i]) % mod;
-
}
-
-
return ret;
-
}
-
-
int main() {
-
// your code
-
}
Input
The first line contains 2 integers n and m, which are the sizes of S1 and S2, respectively. (0 < n,m <= 1000)
Next, there're n lines, each representing a string in S1.
Last, m lines are provided, each representing a string in S2.
The lengths of the strings are not greater than 5*10^4.
Output
Print m lines. Each line contains "Yes" or "No", which means whether the i-th string in S2 exists in S1 or not.
Print '\n' at the end of each line.