Description

Domo is a brilliant dog. By the way, his grandfather is also a brilliant dog, and he has built a giant maze in the forest years ago, which is called "DomoMaze".
One day, Domo loses his ball called Wilson in this maze. He wants to take Wilson back, and your task is to find out how many ways Domo can reach the position where Wilson is.
This DomoMaze can be described as a two-dimensional array. With width W and length L, Domo is at the position (0, 0) in the beginning, and Wilson is at the position (W-1, L-1).
Each time Domo moves, he can choose one of three ways below:
1. from (i, k) to (i+1, k)
2. from (i, k) to (i, k+1)
3. from (i, k) to (i+1, k+1)
Also, there are some portals in the maze. If you step into a certain position (i, k) where has a portal, you will be immediately teleported to the position (i-2, k-2), and the portal you used will disappear.
It is guaranteed that the position (i-2, k-2) is in the DomoMaze, and the portal will not appear at (W-1, L-1).
Given the size of DomoMaze and the position of all portals, please find out how many ways Domo can find Wilson.
Hint: Try to separate the answer to { passing 0 portal, passing 1 portal, passing 2 portals }, and sum all conditions to find the final answer!
We introduced a method called Dynamic Programming.
The main idea is to use the answer of sub-problems to find out the answer to the original problem.
For example, a DomoMaze is given below:

We can calculate how many ways Domo can reach for every position. Obviously, for each position whose index of row or column is 0, there is only 1 way Domo can reach.
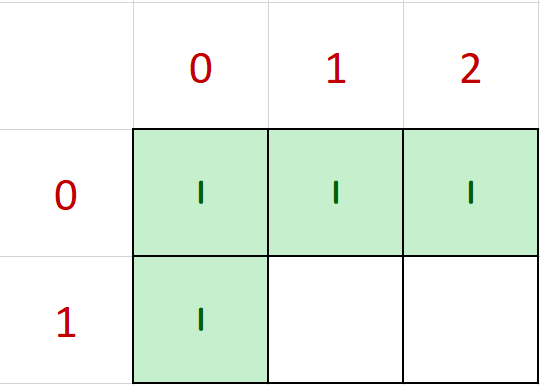
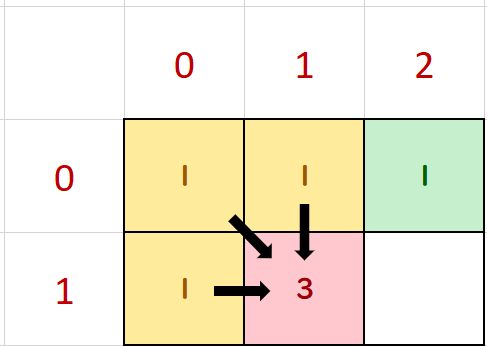
Next, we can calculate the ways Domo can reach the position (1, 1) with the following equation:
f(1, 1) = f(0, 0) + f(1, 0) + f(0, 1)
Hence, there are 3 ways Domo can reach the position (1, 1).
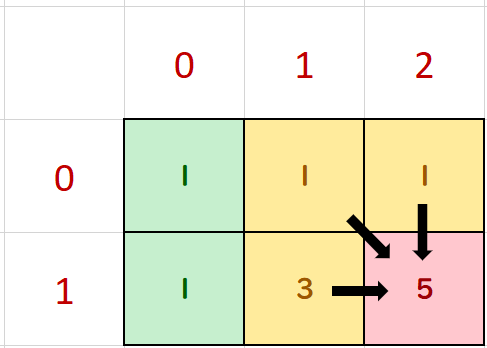
Last step, find the ways Domo can reach (1, 2), which is:
f(1, 2) = f(0, 1) + f(1, 1) + f(0, 2)
You can search dynamic programming on the internet for details if you still have questions.
Reference
English:
Dynamic Programming - GeeksforGeeks
What is the difference between bottom-up and top-down?
Mandarin:
Input
The first line contains two integers W (1 ≤ W ≤ 15) and L (1 ≤ L ≤ 15) - the width and the length of DomoMaze
For the next W lines, each line has L numbers either 1 or 0 - 0 for empty, and 1 for the portal.
The variable range of each test case is different.
For test cases 1 ~ 4, there is no portal in the DomoMaze.
For test case 5, there is one portal in the DomoMaze.
For test case 6, there are two portals in the DomoMaze.
Output
The output only contains a number and a newline character - the number of ways Domo can reach where Wilson is.
It's guaranteed that the answer will not be greater than 231-1.